Алгебра, вопрос задал alineluzhkova16 , 1 год назад

ПОЖАЛУЙСТА, РЕШИТЕ ЭТИ ЗАДАНИЯ ПО АЛГЕБРЕ, СРОЧНО НУЖНА ВАША ПОМОЩЬ! ПОМОГИТЕ
(1)

Приложения:

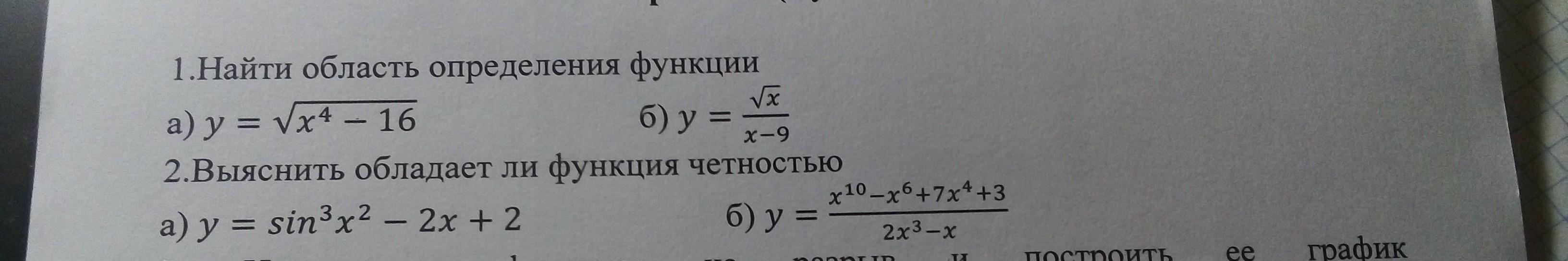
Ответы на вопрос

Ответил nikebod313

$1. \ a) \ y = \sqrt{x^{4} - 16}\\D(y): \ x^{4} - 16 \geq 0; \ x^{4} - 16 = 0; \ x^{4} = 16; \ x = \pm 2;\\x \in (-\infty; -2] \cup [2; +\infty)\\$

$b) \ y = \dfrac{\sqrt{x} }{x - 9};\\D(y): \ \left \{ {\bigg{x \geq 0, \ \ \ \ \ } \atop \bigg{x - 9 \neq 0;}} \right. \ \ \ \ \ \ \ \left \{ {\bigg{x \in [0; +\infty), } \atop \bigg{x \neq 9; \ \ \ \ \ \ \ \ }} \right. \\x \in [0; 9) \cup (9; +\infty)$

$2. \ a) \ y = \sin ^{3}x^{2} - 2x + 2\\y(-x) = \sin ^{3}(-x)^{2} - 2(-x) + 2 = \sin ^{3}x^{2} + 2x + 2 = - (-\sin ^{3}x^{2} - 2x - 2)$

Функция $y(x) \neq y(-x)$ и $y(x) \neq -y(-x)$ , значит, функция $y$ не обладает свойством четности (ни четная, ни нечетная).

$b) \ y = \dfrac{x^{10} - x^{6} + 7x^{4} + 3}{2x^{3} - x} \\y(-x) = \dfrac{(-x)^{10} - (-x)^{6} + 7(-x)^{4} + 3}{2(-x)^{3} - (-x)} = \dfrac{x^{10} - x^{6} + 7x^{4} + 3}{-2x^{3} + x} =\\\\= \dfrac{x^{10} - x^{6} + 7x^{4} + 3}{-(2x^{3} - x)} = -\dfrac{x^{10} - x^{6} + 7x^{4} + 3}{2x^{3} - x} = -y$

Функция является нечетной.

Ответил Аноним

Ответ: во вложении Объяснение:

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

Срочно.яДабо 59 балов...

Қазақ тiлi, 1 год назад

Қазақстан туралы эссе!

Українська мова, 1 год назад

Від поданих імеників утворіть прикметники та підчеркніть слова в яких відбулося спрощення совість, злість, контраст, студент, футурист, якість, честь, кістка,комендант, радість, ненависть, баласт,...

ПОЖАЛУЙСТА, РЕШИТЕ ЭТИ ЗАДАНИЯ ПО АЛГЕБРЕ, СРОЧНО НУЖНА ВАША ПОМОЩЬ! ПОМОГИТЕ(1)

Ответы на вопрос

ПОЖАЛУЙСТА, РЕШИТЕ ЭТИ ЗАДАНИЯ ПО АЛГЕБРЕ, СРОЧНО НУЖНА ВАША ПОМОЩЬ! ПОМОГИТЕ
(1)