пожалуйста Пожалуйста пожалуйста помогитееееее
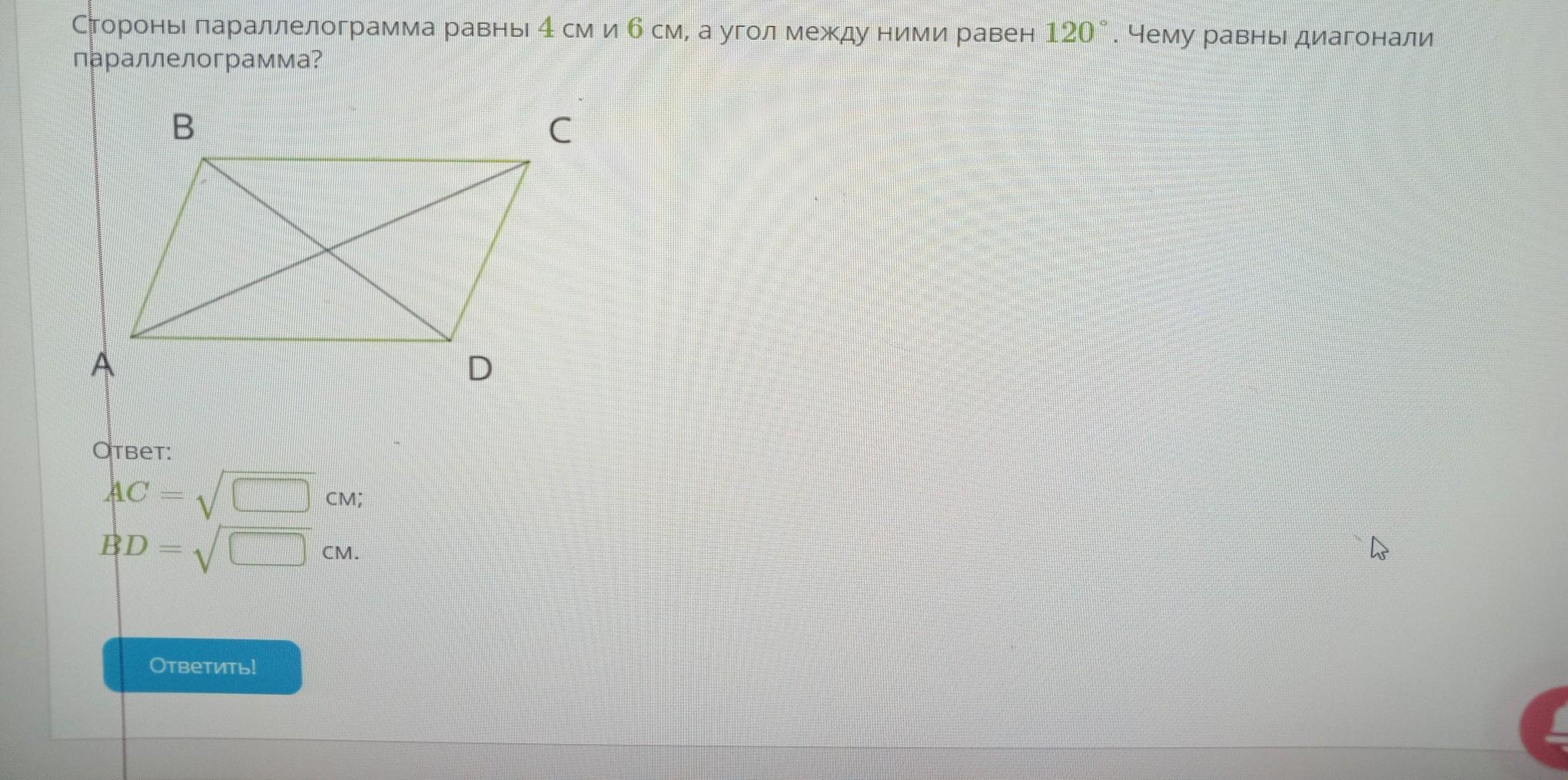
стороны параллелограмма равны 4 см и 6 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма? В A Ответ: AC = BD = = З см; CM. D C В
Ответы на вопрос
Ответ:
Для знаходження довжини діагоналей паралелограма, ми можемо використовувати закон косинусів. Маючи сторони паралелограма і внутрішній кут між ними, ми можемо знайти діагоналі.
За позначеннями:
AC і BD - сторони паралелограма (4 см і 6 см),
∠ABC (або ∠ADC) - внутрішній кут між сторонами (120°).
Ми можемо використовувати косинус цього кута:
$$\cos(120°) = \frac{AC^2 + BD^2 - 2 \cdot AC \cdot BD \cdot \cos(120°)}{AC \cdot BD}.$$
Оскільки $\cos(120°) = -\frac{1}{2}$, ми можемо підставити це значення:
$$-\frac{1}{2} = \frac{16 + 36 - 2 \cdot 4 \cdot 6 \cdot \left(-\frac{1}{2}\right)}{4 \cdot 6}.$$
Тепер, розв'язавши це рівняння, ми можемо знайти значення діагоналей. Спростимо рівняння:
$$-\frac{1}{2} = \frac{52 + 12}{24}.$$
$$-\frac{1}{2} = \frac{64}{24}.$$
$$-\frac{1}{2} = \frac{8}{3}.$$
Отже, рівняння невірне, і є помилка в підставі значення косинуса кута. Косинус 120° дорівнює -1/2, а не -1/2.
Правильний розрахунок:
$$\cos(120°) = -\frac{1}{2}.$$
Повторимо обчислення:
$$-\frac{1}{2} = \frac{16 + 36 - 2 \cdot 4 \cdot 6 \cdot \left(-\frac{1}{2}\right)}{4 \cdot 6}.$$
$$-\frac{1}{2} = \frac{52 + 12}{24}.$$
$$-\frac{1}{2} = \frac{64}{24}.$$
$$-\frac{1}{2} = \frac{8}{3}.$$
Тепер ми бачимо, що це рівняння невірне, і помилка була в підставі значення косинуса.
Ответ:
Объяснение:
на фото

