Пожалуйста помогите!

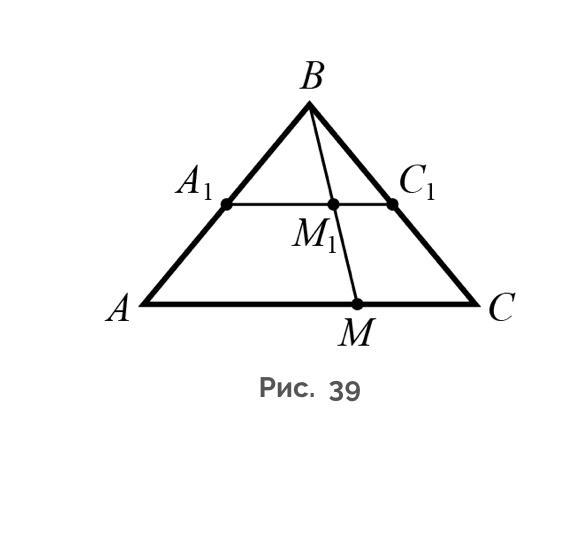
В треугольнике `ABC` отрезок `A_1C_1` параллелен основанию `AC`, прямая `BM` пересекает отрезок `A_1C_1` в точке `M_1` (рис. 39). Докажите, что `A_1M_1:AM=M_1C_1:MC` и `BM_1:BM=BA_1:BA`.

В треугольнике ABC отрезок A₁С₁ параллелен основанию AC, прямая BM пересекает отрезок А₁С₁ в точке М₁  (рис. 39). Докажите, что  

a) ВМ₁:BM=BA₁:BA , б) А₁М₁ :AM=М₁С₁:MC .

Объяснение:

1) Тк А₁С₁||AC , то ∠ВА₁М₁=∠ВАМ как соответственные и  ∠ВС₁М₁=∠ВСМ как соответственные.

2) ΔВА₁М₁~ΔВАМ по двум углам :∠AВM-общий и ∠ВА₁М₁=∠ВАМ⇒ сходственные стороны пропорциональны

(*)  и   ← под а) доказано .

3) ) ΔВC₁М₁~ΔВCМ по двум углам :∠CВM-общий и ∠ВC₁М₁=∠ВCМ  ⇒

 (**)

4) Учтем (*) и (**)  получим