ПОЖАЛУЙСТА ПОМОГИТЕ СРОЧНО РЕШИТЬ
Определи значение выражения:
3x−1−y−13x−1+y−1, если yx=4−1.
Ответ (минус пиши в числителе):
3x−1−y−13x−1+y−1=
Ответы на вопрос
Ответил axatar
2
Ответ:
Объяснение:
Верное условие (см. рисунок):
Определи значение выражения при
Сначала изменим вид дроби:
Теперь подставляем :
Приложения:
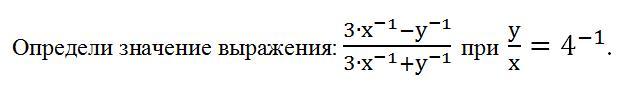
Новые вопросы
Английский язык,
1 год назад
Русский язык,
1 год назад
Математика,
2 года назад
Математика,
2 года назад