Алгебра, вопрос задал gopuka9572 , 1 год назад

Пожалуйста помогите сделать задание по алгебре

Приложения:

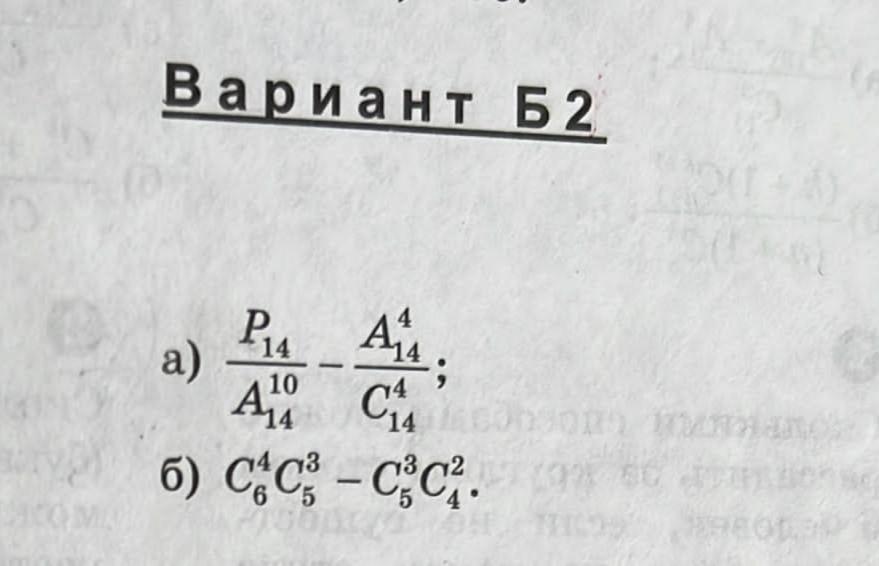
Ответы на вопрос

Ответил NNNLLL54

0

Ответ:

Вычислить . Применяем формулы : $\bf P_{n}=n!=1\cdot 2\cdot ...\cdot n\ \ ,$

$\bf A_{n}^{k}=\dfrac{n!}{(n-k)!}\ \ ,\ \ \ C_{n}^{k}=\dfrac{A_{n}^{k}}{k!}=\dfrac{n!}{k!\, (n-k)!}$ .

$\bf a)\ \ \dfrac{P_{14}}{A_{14}^{10}}-\dfrac{A_{14}^4}{C_{14}^4}=\dfrac{14!}{\dfrac{14!}{4!}}-\dfrac{A_{14}^4}{\dfrac{A_{14}^4}{4!}}}=4!-4!=0$

$\bf b)\ \ C_6^4\cdot C_5^3-C_5^3\cdot C_4^2=\dfrac{6!}{4!\, 2!}\cdot \dfrac{5!}{3!\, 2!}-\dfrac{5!}{3!\, 2!}\cdot \dfrac{4!}{2!\, 2!}=\\\\\\=\dfrac{4!\, \cdot 5\cdot 6}{4!\, 2!}\cdot \dfrac{3!\, \cdot 4\cdot 5}{3!\, 2!}-\dfrac{3!\, \cdot 4\cdot 5}{3!\, 2!}\cdot \dfrac{2!\, \cdot 3\cdot 4}{2!\, 2!}=\dfrac{5\cdot 6}{2!}\cdot \dfrac{4\cdot 5}{2!}-\dfrac{4\cdot 5}{2!}\cdot \dfrac{3\cdot 4}{2!}=\\\\\\=(5\cdot 3)\cdot (2\cdot 5)-(2\cdot 5)\cdot (3\cdot 2)=15\cdot 10-10\cdot 6=10\cdot (15-6)=10\cdot 9=90$

Приложения:

masha01021: здравствуйте, помогите пожалуйста решить задачу

masha01021: интегралы

Ответил сок111213

1

Решение на прикреплённой фотографии

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 1 год назад

Яку масу ферум (III) оксиду можна розчинити у розчині масою 392г з масовою часткою сульфатної кислоти 2%?

История, 1 год назад

БУДЬ ЛАСОЧКА!!!!!ВИКОНАЙТЕ...

Русский язык, 1 год назад

149. Творческое упражнение. Продолжите предложения. 1. Какие бы мысли ни приходили ему в голову... 2. Кто бы к нам ни приходил... 3. Кто к нам не приходил... 4. Что бы там ни про- исходило... 5. Что...

Алгебра, 1 год назад

3. Решите уравнения: a) 0,5a + 11 = 4 - За b) 6x — (7x — 12) = 101 c) 2x + 5 = 2(x + 1) + 11...

Право, 6 лет назад

по познанию мира какие катаклизмы характерны для Карагандинской местности...

Математика, 6 лет назад

Одна сторона прямоугольника равна 51см соседняя - в 3 раза меньше. Найдите площадь прямоугольника.