Алгебра, вопрос задал saturnating , 1 год назад

пожалуйста, помогите с решение.

Приложения:

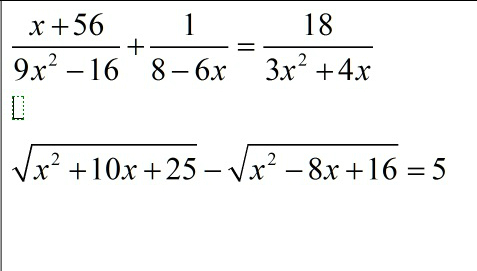
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$1)\ \ \dfrac{x+56}{9x^2-16}+\dfrac{1}{8-6x}=\dfrac{18}{3x^2+4x}$

Раскладываем знаменатели на множители и определяем общий знаменатель .

$\displaystyle \frac{x+56}{(3x-4)(3x+4)}+\frac{1}{-2\, (3x-4)}=\frac{18}{x\, (3x+4)}\\\\\\\frac{2x(x+56)-x(3x+4)-18\cdot 2(3x-4)}{2x\, (3x-4)(3x+4)}=0\ \ ,\ \ ODZ:\ x\ne 0\ ,\ x\ne \frac{4}{3}\ ,\ x\ne -\frac{4}{3} \\\\\\\frac{2x^2+112-3x^2-4x-108x+144}{2x\, (3x-4)(3x+4)}=0\\\\\\\frac{-x^2-112x+256}{2x\, (3x-4)(3x+4)}=0$

$\dfrac{x^2+112x-256}{2x\, (3x-4)(3x+4)}=0\ \ \ \Rightarrow \ \ \ x^2+112x-256=0\ \ ,\\\\\\D/4=(b/2)^2-ac=56^2+256=3392=64\cdot 53\\\\\boldsymbol{x_1=-56-8\sqrt{53}\ \ , \ \ x_2=-56+8\sqrt{53}}\ \ \ -\ otvet$

$2)\ \ \sqrt{x^2+10x+25}-\sqrt{x^2-8x+16}=5\\\\\sqrt{(x+5)^2}-\sqrt{(x-4)^2}=5\ \ ,\ \ \ ODZ:\ \left\{\begin{array}{l}(x+5)^2\geq 0\\(x-4)^2\geq 0\end{array}\right\ \ \Rightarrow \ \ x\in R\\\\|x+5|-|x-4|=5$

Рассмотрим три промежутка: (-∞;-5] , (5;4] , (4;+∞) . На каждом из этих промежутков раскроем модули .

$|x+5|=\left[\begin{array}{l}-x-5\ ,\ esli\ \ x\leq -5\ ,\\x+5\ ,\ esli\ x > -5\end{array}\right\ \ ,\ \ |x-4|=\left[\begin{array}{l}-x+4\ ,\ esli\ \ x\leq 4\ ,\\x-4\ ,\ esli\ x > 4\end{array}\right$

$a)\ \ x\in (-\infty ;\, -5\ ]:\ \ -x-5-(-x+4)=5\ \ ,\ \ -x-5+x-4=5\ \ ,$

$-9=5$ неверное утверждение, поэтому на этом промежутке нет решений , $x\in \varnothing$

$b)\ \ x\in (-5\, ;\ 4\ ]:\ \ x+5-(-x+4)=5\ \ ,\ \ 2x+1=5\ \ ,\ \ 2x=4\ ,\\\\\boldsymbol{x=2}\in (-5\, ;\ 4\ ]\\\\c)\ \ x\in (\ 4\ ;+\infty ):\ \ x+5-(x-4)=5\ \ ,\ \ x+5-x+4=5\ ,$