Пожалуйста помогите решить очень нужно

Ответы на вопрос
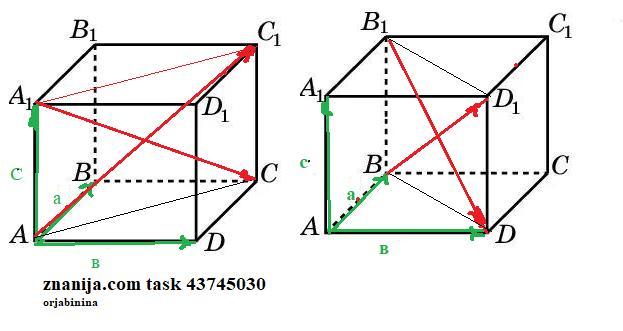
В параллелепипеде АВСDА1В1С1D1 даны векторы АВ=а, АВ=в,АА1=с , совпадающие с его ребрами .Найти векторы -диагонали АС1, А1С, ВD1,B1D .
Объяснение:
1) Вектор АС1 , по правилу параллелограмма в плоскости (АСС1) , равен
АС1=с+АС= (по правилу параллелограмма вектор АС плоскости (АВС) равен )
АС1=с+(а+в)=а+в+с
2)Вектор А1С , по правилу разности векторов в плоскости (АСС1) , равен А1С=с-АС= (по правилу параллелограмма вектор АС плоскости (АВС) равен )
АС1=с-(а+в)= с-а-в.
3)Вектор ВD1, по правилу параллелограмма в плоскости (ВВ1D1) , равен
ВD1=ВВ1+ВD= ( вектор ВВ1=АА1=а ; по правилу разности вектор ВD=в-а в плоскости (АВС) )
ВD1 =с-(в-а)=с-в+а=а-в+с.
4)Вектор В1D, по правилу параллелограмма в плоскости (ВВ1D1) , равен
В1D=В1В+В1D1= ( вектор В1В=-АА1= -с ; вектор В1D1=ВD=в-а )
В1D =-с+в-а=в-а-с.