Пожалуйста, помогите!!!! Очень срочно!!!!
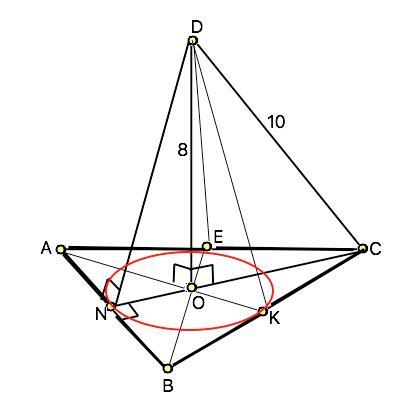
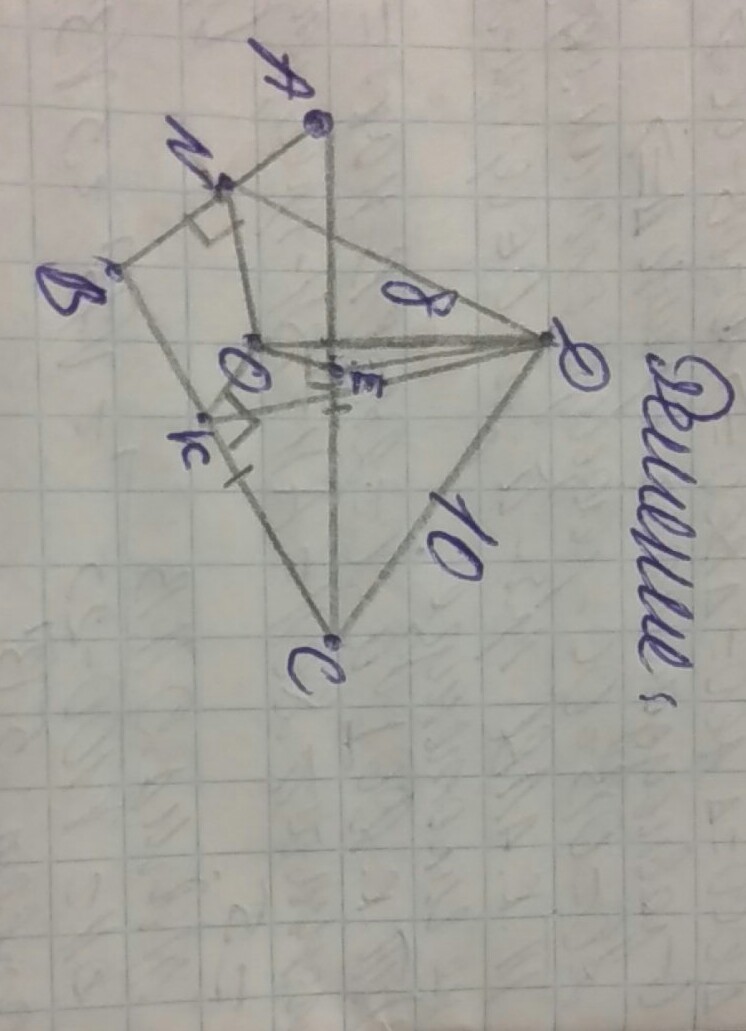
2)тр-ик ABC, AB=BC=AC, O - центр тр-ка ABC, DO перп-н (ABC), DC=10,DO=8. Найти: S abc, расст-е от точки D до сторон тр-ка ABC. (Рисунок мой ☝)

Ответ: S=27√3 (ед. площади), DN=√73 (ед. длины)

Объяснение:

  АВ=АС=ВС (дано) ⇒ ∆ АВС  равносторонний. DО перпендикуляр к плоскости треугольника. Прямая, перпендикулярная плоскости, перпендикулярна каждой прямой, лежащей в данной плоскости. ⇒

∆ DОС - прямоугольный с отношением катет: гипотенуза 8:10=4:5 ( египетский), поэтому катет ОС=6. (Можно вычислить по т.Пифагора).  

  Точка О, как центр правильного треугольника, является точкой пересечения его медиан ( в правильном треугольнике ещё высот и биссектрис) и делит их в отношении 2:1, считая от вершины. СО=6 => ОN=6:2=3, высота СN=CO+ON=9.  

  Площадь равностороннего треугольника через высоту

S=h²/√3=81/√3=27√3 (можно по формуле а=h/sin60° вычислить длину стороны ∆ АВС и S=a•h:2)

 Т.к. О - центр треугольника, расстояние от О до сторон ∆ АВС равно радиусу вписанной окружности, и  расстояние от D до всех сторон данного равностороннего треугольника  одинаково.

Расстояние от точки (D) до прямой (АВ) равно длине отрезка, проведенного между ними перпендикулярно. СN - перпендикулярно АВ ( высота), ⇒ по т. о 3-х перпендикулярах DN перпендикулярно АВ.  Из прямоугольного треугольника DON по т.Пифагора гипотенуза DN=√(NO²+DO²)=√(8²+3²)=√73 (ед. длины)