пожалуйста помогите,даю 30 баллов.
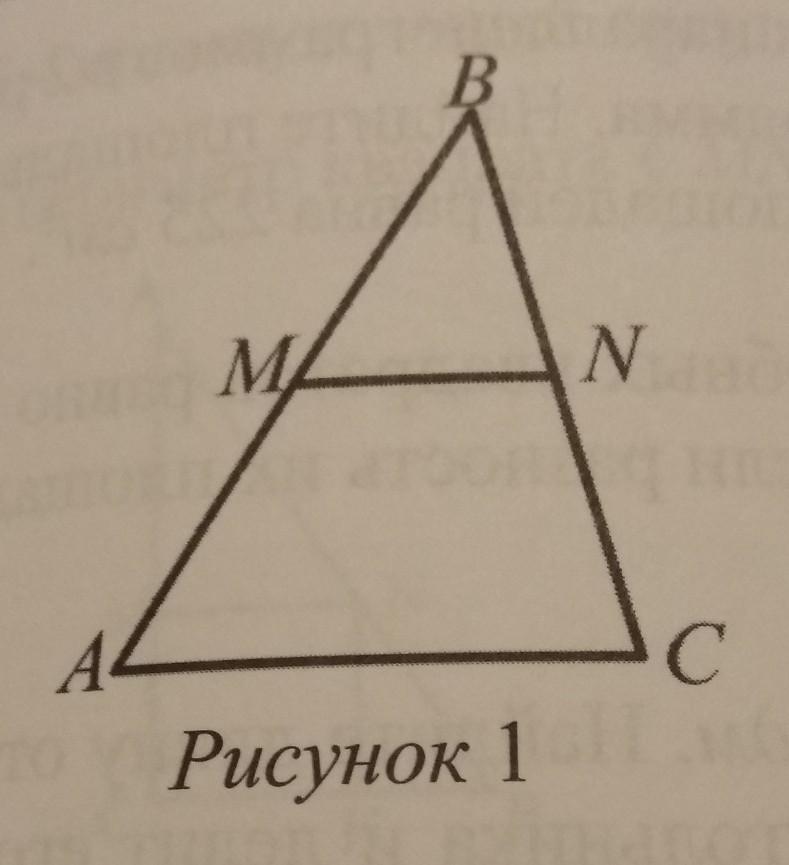
В треугольнике ABC, MN является средней линией. Найдите площадь треугольника ABC, если площадь треугольника MBN равен 18 см².
Приложения:
Ответы на вопрос
Ответил Nimastel
2
Ответ:
72 см^2
Пошаговое объяснение:
ΔABC подобен ΔMBN (∠B - общий, ∠CAB = ∠NMB)
Теорема: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
.
⇒
(так как средняя линия равна половине основания).
⇒
(см^2)
Ответил solyanine
1
Ответ:
Пошаговое объяснение:
Приложения:
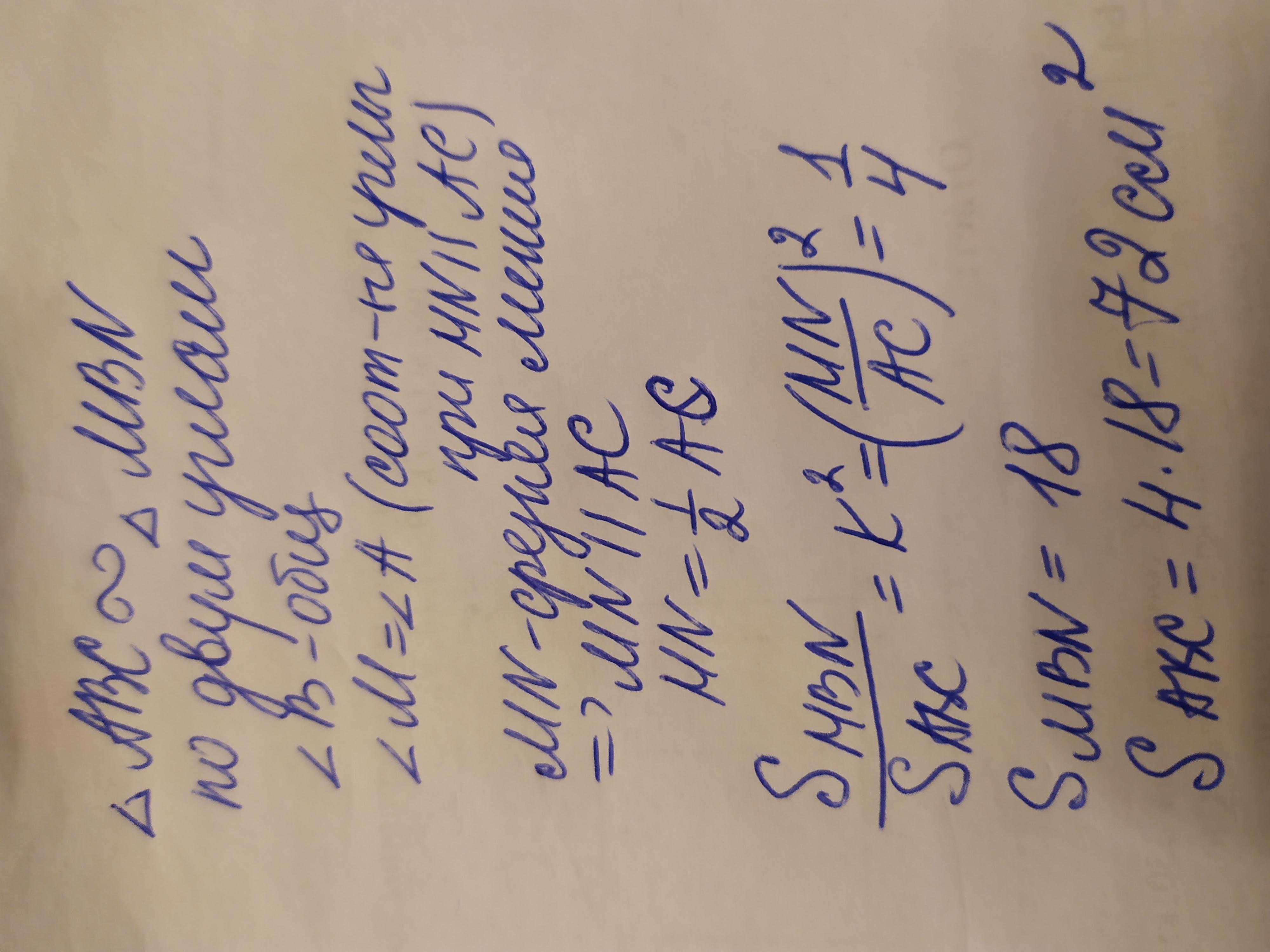
Новые вопросы