Алгебра, вопрос задал biathlonworld01 , 7 лет назад

Пожалуйста, объясните, как решить номер 1262

Приложения:

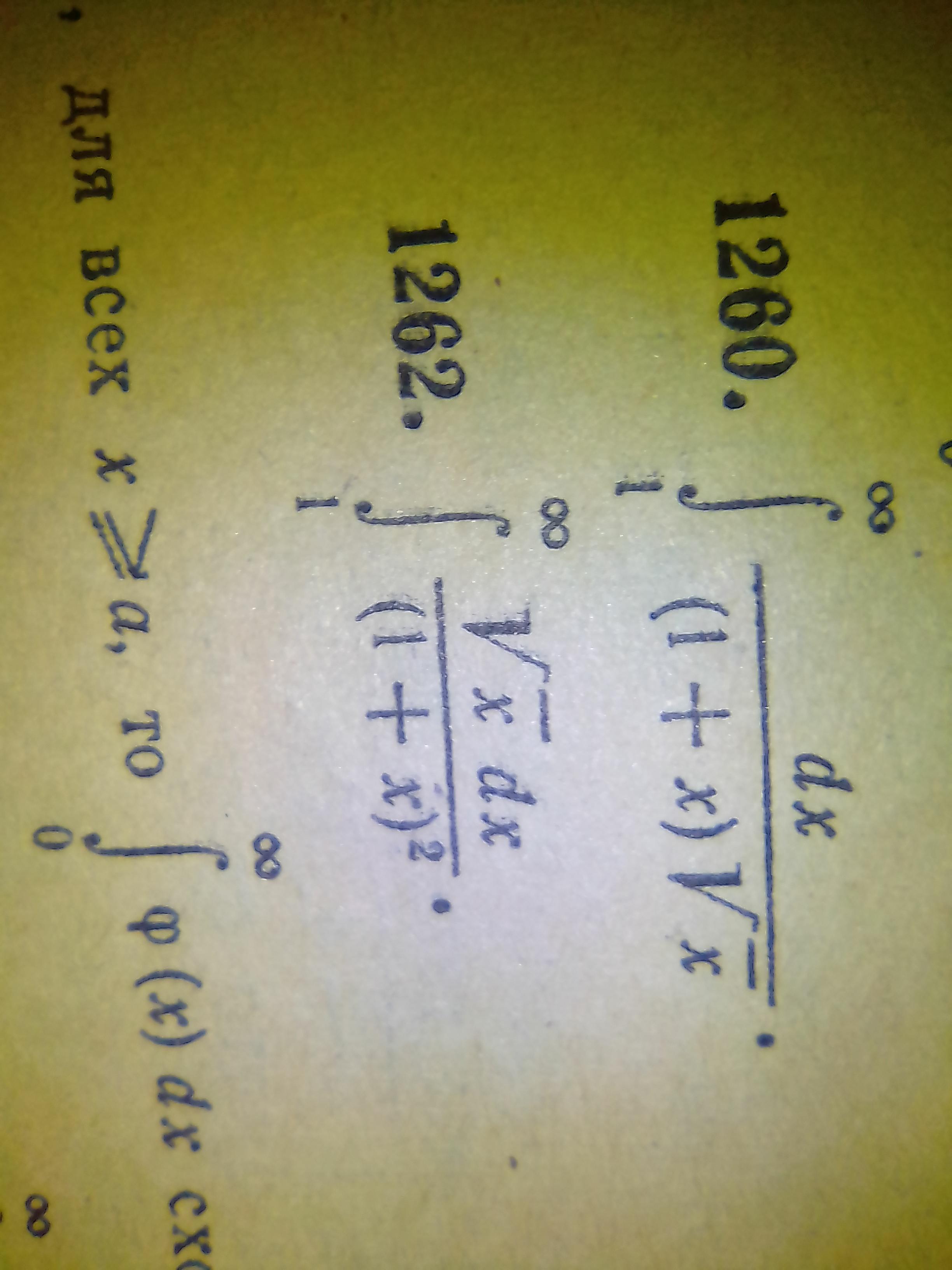
Ответы на вопрос

Ответил alkorb

Ответ:

$frac{pi+2}{4}$

Объяснение:

Сделаем замену переменных:

$sqrt{x} =t \ x=t^2 \ dx=2tdt$

также сразу заменим пределы интегрирования, чтобы не возвращаться к обратной замене:

нижний предел:

$x=1 Rightarrow t=sqrt{x}=sqrt{1}=1$

Верхний предел:

$xrightarrow infty Rightarrow t= sqrt{x}rightarrow sqrt{ infty}= infty$

Получаем:

$intlimits^ infty_1 {frac{sqrt{x}dx }{(1+x)^2} } =intlimits^infty_1 {frac{t*2tdt}{(1+t^2)^2} } =intlimits^infty_1 {frac{2t^2dt}{(1+t^2)^2} } =(*)$

Полученный интеграл не является табличным, поэтому для его решения нужно упростить знаменатель:

Когда в знаменателе стоят выражения 1) 1+x² или 2) 1-x² применяют тригонометрическую или гиперболическую замены.

Для первого случая применяют (на выбор): x=tgt; x=ctgt; x=sht.

Для второго: x=sint; x=cost

В нашем случае применим замену (да, еще одну, такое тоже бывает!)

$t=tgz; \ \ dt=frac{1}{cos^2z} dz$

Также заменим пределы интегрирования:

$t=1 Rightarrow 1=tgz Rightarrow z=frac{pi }{4} \ \ trightarrow infty Rightarrow infty=tgz Rightarrow z rightarrow frac{pi}{2}$

Итого имеем:

$(*)=intlimits^{frac{pi}{2} }_{frac{pi}{4} } {{frac{2tg^2z*frac{1}{cos^2z}dz }{(1+tg^2z)^2} }} = intlimits^{frac{pi}{2} }_{frac{pi}{4} } {{frac{2tg^2zdz}{cos^2z(1+tg^2z)^2} }} =(**)$

Учитывая, что 1+tg²z=1/cos²z; tg²z=sin²z/cos²z; 2sin²z=1-cos(2z)

Получаем:

$(**)= intlimits^{frac{pi}{2} }_{frac{pi}{4} } {{frac{2frac{sin^2z}{cos^2z} dz}{cos^2z(frac{1}{cos^2z} )^2} }} =intlimits^{frac{pi}{2} }_{frac{pi}{4} } {{frac{2sin^2zdz}{cos^4zfrac{1}{cos^4z}} }} =intlimits^{frac{pi}{2} }_{frac{pi}{4} }2sin^2zdz=intlimits^{frac{pi}{2} }_{frac{pi}{4} }(1-cos2z)dz= \ \ =limlimits_{brightarrow frac{pi}{2}}(z-frac{1}{2} sin2z)|^b_{frac{pi}{4}}=limlimits_{brightarrow frac{pi}{2}}(b-frac{1}{2} sin2b-frac{pi}{4}}+frac{1}{2}sinfrac{pi}{2}})=$

$frac{pi}{2}}-frac{1}{2} sinpi-frac{pi}{2}}+frac{1}{2}sinfrac{pi}{2} = frac{pi}{2}}-0-frac{pi}{4}}+frac{1}{2}} =frac{pi +2}{4}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Помогите с английским...

Русский язык, 1 год назад

фонетический разбор слова зойка и сойка...

Математика, 7 лет назад

6 см 6 мм × 2 2 ц 5 кг ×3...

Биология, 7 лет назад

для чего нужен рентген...

Математика, 8 лет назад

если 1 декабря - среда то число будет в последнюю среду декобря...

География, 8 лет назад

какими были предпосылки наступления эпохи великих географических открытий ? помогите пожалуйста! в зарание спасибо!