пожалуйста, напишите решение этих примеров, сколько сможете
Ответы на вопрос
ответы:
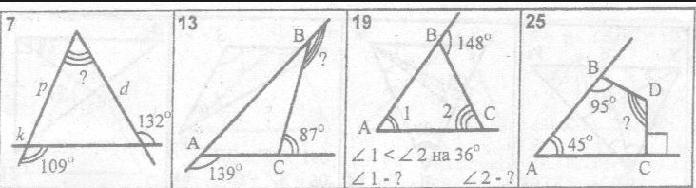
7. 61°
13. 134°
19. ∠1 = 56°; ∠2 = 92°
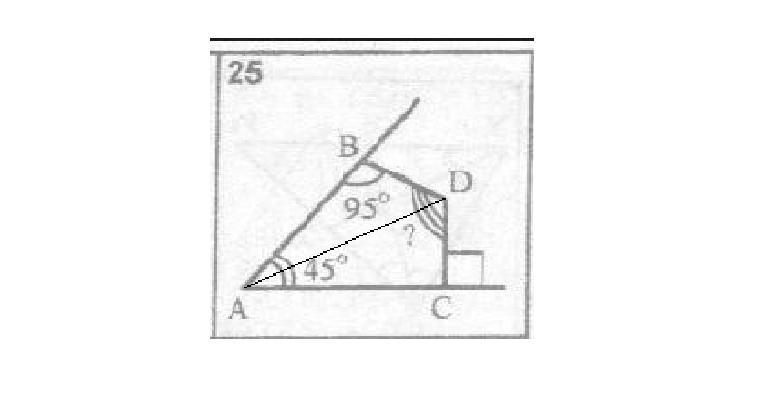
25. 130°
объяснение:
(возможно мои объяснения могут показаться вам непонятными, если чего-то не поняли, спрашивайте)
7. 180° - 132° = 48°
180° - 109° = 71°
сумма всех углов треугольника равна 180°. из этого следует, что
180° - (48° + 71°) = 61° - это мы нашли неизвестный угол
13. ∠АСВ = 180° - 87° = 93°
∠ВАС = 180° - 139° = 41°
сумма всех углов треугольника равна 180°, значит
∠АВС = 180° - (93° + 41°) = 46°
чтобы узнать неизвестный угол надо 180° - 46° = 134°
19. ∠АВС = 180° - 148° = 32°
сумма всех углов треугольника равна 180° ⇒
180° - 32° = 148° - сумма ∠1 и ∠2
т.к. ∠1 < ∠2 на 36°, можно составить уравнение
х + (х + 36°) = 148°
2х + 36° = 148°
2х = 112°
х = 56°
∠1 = 56°
∠2 = 56° + 36° = 92°
25. если провести биссектрису ∠А (на картинке ниже показано), то ∠А поделится на пополам, т.е 45° : 2 = 22,5° - каждая половинка
фигура делится на два треугольника, △АВD и △ACD.
опять таки, сумма всех углов треугольника равна 180° ⇒
180° - (95° + 22,5°) = 62,5° - ∠BDA
по картинке можно определить, что ∠DCA = 90°
180° - (90° + 22,5°) = 67,5° - ∠CDA
∠D = 62,5° + 67,5° = 130°