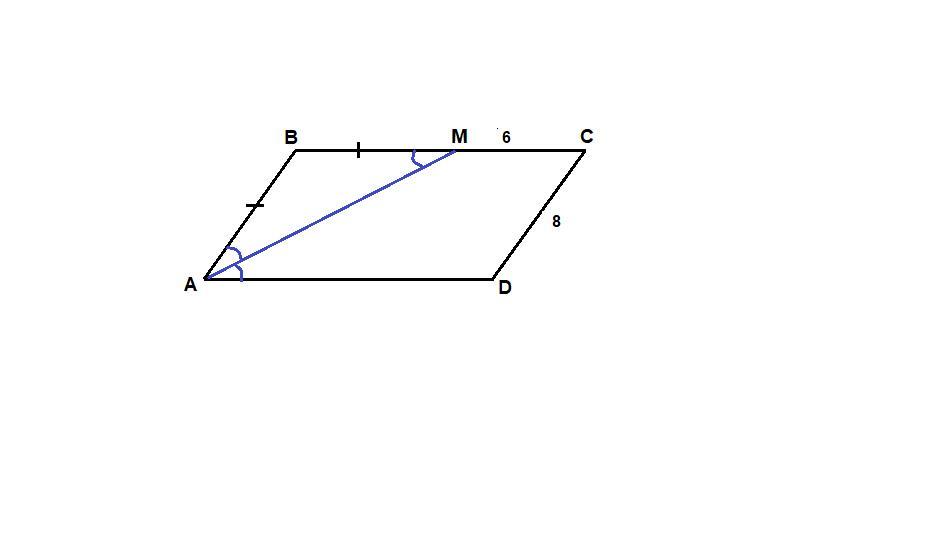
ПОЖАЛУЙСТА! На стороне BC параллелограмма ABCD взята точка M так, что AB=BM. a) Докажите, что AM -- биссектриса угла BAD. б) Найдите периметр параллелограмма, если CD=8 см, a CM=6 см.

a)Т. к. АМ = BM, то треуг. ABM - равнобедренный с основанием AM. Углы при основании равны => угол BAM = углу BMA.

Т к это параллелограмм, то противоположные стороны параллельны, т е BC || AD. Углы BMA и MAD - накрестлежащие (BC || AD, MC - секущая), следовательно они тоже равны. Получаем что угол BAM = углу MAD, следовательно MA - биссекрисса угла BAD.

б) CD=8=AB.

AD=BC= BM + CM = 8 + 6 = 14

P = 14*2 + 8*2 = 28 + 16 =44

Ответ:

         б) 14 см

Объяснение:

а) ∠BAM = ∠BMA как углы при основании равнобедренного треугольника ВАМ,

∠ВМА = ∠DAM как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АМ, ⇒

∠ВАМ = ∠DAМ, ⇒

АМ - биссектриса угла BAD.

б) ВМ = АВ = CD = 8 см

ВС = BM + CM = 8 + 6 = 14 см

Pabcd = (AB + BC) · 2 = (8 + 14) · 2 = 44 см