Геометрия, вопрос задал Merrick8 , 1 год назад

Потрібно повне пояснення, бажано на фото

Приложения:

Ответы на вопрос

Ответил ReMiDa

Ответ:

2) Медіана ВМ дорівнює 2√10.

3) Довели, що трикутник АВС рівнобедрений.

Объяснение:

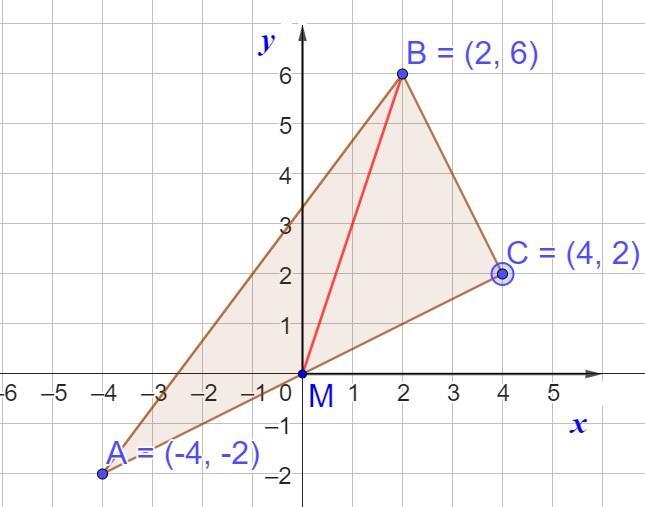
№2. Знайдіть медіану ВМ трикутника, вершинами якого є точки А(-4; -2), В(2; 6), С(4; 2).

Медіана трикутника - відрізок, який виходить з вершини трикутника і ділить протилежну сторону навпіл, тобто AM=MC (див.рис.)

Знайдемо координати середини відрізка AC, тобто координати точки M за формулами:

$\boxed{\bf x_M=\dfrac{x_A+x_C}{2} ; \;\;\;\;y_M=\dfrac{y_A+y_C}{2} }$

$x_M=\dfrac{-4+4}{2} =\bf 0$

$y_M=\dfrac{-2+2}{2} =\bf 0$

Звідси M(0; 0).

Знайдемо довжину відрізка (медіани) BM - відстань між точками B і M за формулою:

$\boxed{\bf \mid BM \mid =\sqrt{(x_M-x_B)^{2}+(y_M-y_B)^{2} } }$

$\mid BM \mid =\sqrt{(0-2)^{2}+(0-6)^{2} } =\sqrt{4+36} =\sqrt{40} =\bf 2\sqrt{10}$

№3. Доведить, що трикутник АВС є рівнобедреним, якщо А(2; -3), В(3;0), С(-1; -2).

Рівнобедрений трикутник - це трикутник, у якого дві сторони рівні.

Обчислимо довжини сторін трикутника АВС за формулою:

$\boxed{\bf AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^{2} } }$

де х₁, х₂, у₁, у₂ - координати точок А(х₁;у₁) та В(х₂;у₂).

$AB=\sqrt{(3-2)^2+(0-(-3))^{2} }=\sqrt{1^{2}+3^2 } =\sqrt{1+9} =\bf\sqrt{10}$

$BC=\sqrt{(-1-3)^2+(-2-0)^{2} }=\sqrt{(-4)^{2}+(-2)^2 } =\sqrt{16+4} =\bf\sqrt{20}$ $AC=\sqrt{(-1-2)^2+(-2-(-3))^{2} }=\sqrt{(-3)^{2}+1^2 } =\sqrt{9+1} =\bf\sqrt{10}$

Так як ВС=АС=√10, то △АВС - рівнобедрений.

#SPJ1

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 11 месяцев назад

Елемент утворює летку сполуку з Гідрогеном H3E, у якій масова частка його 91,17%. Який це елемент?

Математика, 11 месяцев назад

505. Қайық көлде жүзіп, 3 сағатта қандай қашықтыққа барса, Сал осы өзенде 1 сағатта осы қашықтықтың қандай бөлігіне жүзіп барады? 1 1 506. Домбыраның басы (құлағы) М, МОЙНЫ 10 2 Домбыраның ұзындығы...

Українська мова, 1 год назад

9. Установіть відповідність між видом односкладного реченням та прикладом 1. означено-особове А Снігом замело дорогу. 2. неозначено-особове Б Чесне діло роби сміло. 3. узагальнено-особове В На...

Геометрия, 1 год назад

№8 Довжина бічних сторін рівнобедреного трикутника ,кут між якими 30°, дорівнює 20 см. Знайдіть площу цього трикутника. Ваша відповідь:...

Алгебра, 6 лет назад

4. (5 балла] Решите неравенство (у – 2)(у + 3) - (y-2)² > 25...

Математика, 6 лет назад

Дано трикутник АВС, кут С=90º, AB =20 см, косинус кута 4 = 0,7 Знайти сторону AC...