Постройте треугольник,вершинами которого являются точки А(-3;0) B(0;2) C(6;0). Задайте этот треугольник системой неравенств и определить его площадь
Ответы на вопрос
Ответил nafanya2014
0
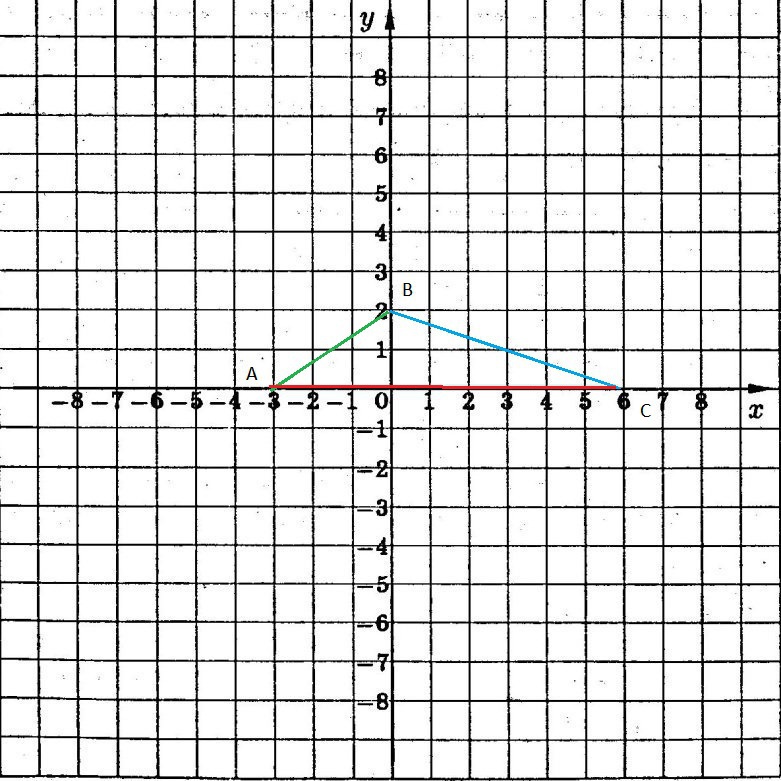
См. рисунок в приложении.
Уравнение прямой АВ:
у=kх+b
Подставляем координаты точки В(0;2)
2=0+b ⇒ b = 2
у=kx+2
Подставляем координаты точки А(-3;0)
0=-3k+2
k=2/3
Прямая у=(2/3)x+2 делит координатную плоскость на две части
у≤(2/3)х+2 и у=(2/3)х+2
Проверим какой из них принадлежит точка (0;0)
0≤2 - верно
Значит, она из трех неравенств для треугольника
у≤(2/3)х+2
Составим уравнение прямой ВС:
у=кх+2
С(6;0)
0=6k+2
k=-1/3
у≤-1/3k+2 - второе неравенство
Уравнение прямой АС- уравнение оси Ох
у=0
у≥0 - третье неравенство.
S( Δ ABC) = AC·BO/2=9·2/2=9 кв. ед.
Система неравенств:
{у≤(2/3)х+2
{у≤-1/3k+2
{у≥0.
Уравнение прямой АВ:
у=kх+b
Подставляем координаты точки В(0;2)
2=0+b ⇒ b = 2
у=kx+2
Подставляем координаты точки А(-3;0)
0=-3k+2
k=2/3
Прямая у=(2/3)x+2 делит координатную плоскость на две части
у≤(2/3)х+2 и у=(2/3)х+2
Проверим какой из них принадлежит точка (0;0)
0≤2 - верно
Значит, она из трех неравенств для треугольника
у≤(2/3)х+2
Составим уравнение прямой ВС:
у=кх+2
С(6;0)
0=6k+2
k=-1/3
у≤-1/3k+2 - второе неравенство
Уравнение прямой АС- уравнение оси Ох
у=0
у≥0 - третье неравенство.
S( Δ ABC) = AC·BO/2=9·2/2=9 кв. ед.
Система неравенств:
{у≤(2/3)х+2
{у≤-1/3k+2
{у≥0.
Приложения:
Новые вопросы