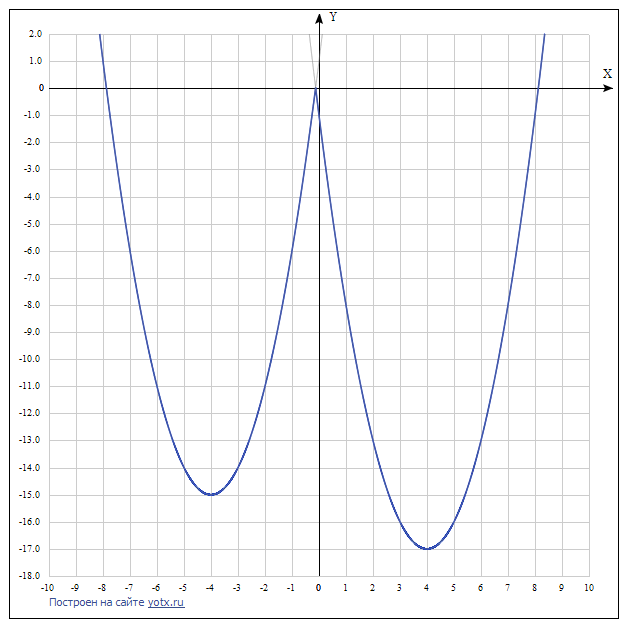
Алгебра, вопрос задал daniel002 , 1 год назад

Постройте график функции
y=x^2- [8x+1]
и определите, при каких значениях m
прямая y=m имеет с графиком ровно три общие точки.

Ответы на вопрос

Ответил arsenlevadniy

77

$y=x^2- |8x+1|, \\ y= \left [ {{x^2-(8x+1), 8x+1 \geq 0,} \atop {x^2+(8x+1), 8x+1\ \textless \ 0;}} \right. \\ y= \left [ {{x^2-8x-1, x \geq - \frac{1}{8} ,} \atop {x^2+8x+1, x \ \textless \ - \frac{1}{8};}} \right. \\ y= \left [ {{(x-4)^2-17, x \geq - \frac{1}{8} ,} \atop {(x+4)^2-15, x \ \textless \ - \frac{1}{8}.}} \right. \\ -15 \leq m \leq 0.$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

фонетический разбор слова касаться...

Обществознание, 1 год назад

Помогите прокоментировать 3 цитаты пожалуйста ...

Русский язык, 1 год назад

разберите слово по составу кроссовки...

Геометрия, 1 год назад

ПОМОГИТЕ!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!CРОЧНО!!!!!!!РЕШИТЕ,ПОЖАЛУЙСТА!!!!!!!СОВСЕМ НЕ ПОНИМАЮ!!!!!!!!!!!!!!

Физика, 7 лет назад

Чему равна площадь опоры кирпичной стены, если ее высота 4м, а давление, которое она оказывает на землю составляет 50 кПа? Плотность кирпича 1600 кг/м3(кубический)...

Алгебра, 7 лет назад

Найдите все значения числа а,при которых уравнение (а+5)х×х-(а+6)х+3=0 имеет один корень! СРОЧНО!ПОМОГИТЕ!