Алгебра, вопрос задал maymr , 1 год назад

Постройте график функции (на картинке).

Определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.

Приложения:

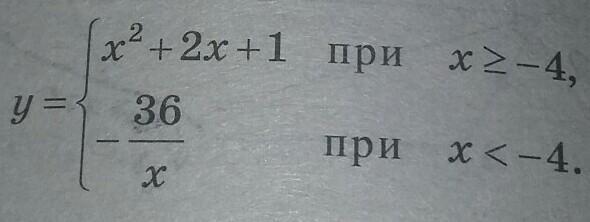
Ответы на вопрос

Ответил igundane

$f(x)=x^2+2x+1\\f(x)=(x+1)^2\\Ox:x=-1\\Oy:y=1\\.........\\g(x)=-\frac{36}{x} \\Ox: -\\Oy: -\\$

Найдём точки пересечения:

$f(x)=g(x)\\x^2+2x+1=-\frac{36}{x} <=>x^3+2x^2+x+36=0<=>(x+4)(x^2-2x+9)=0\\x=-4=>y=9$

Обязательно нужно не забыть про ограничения

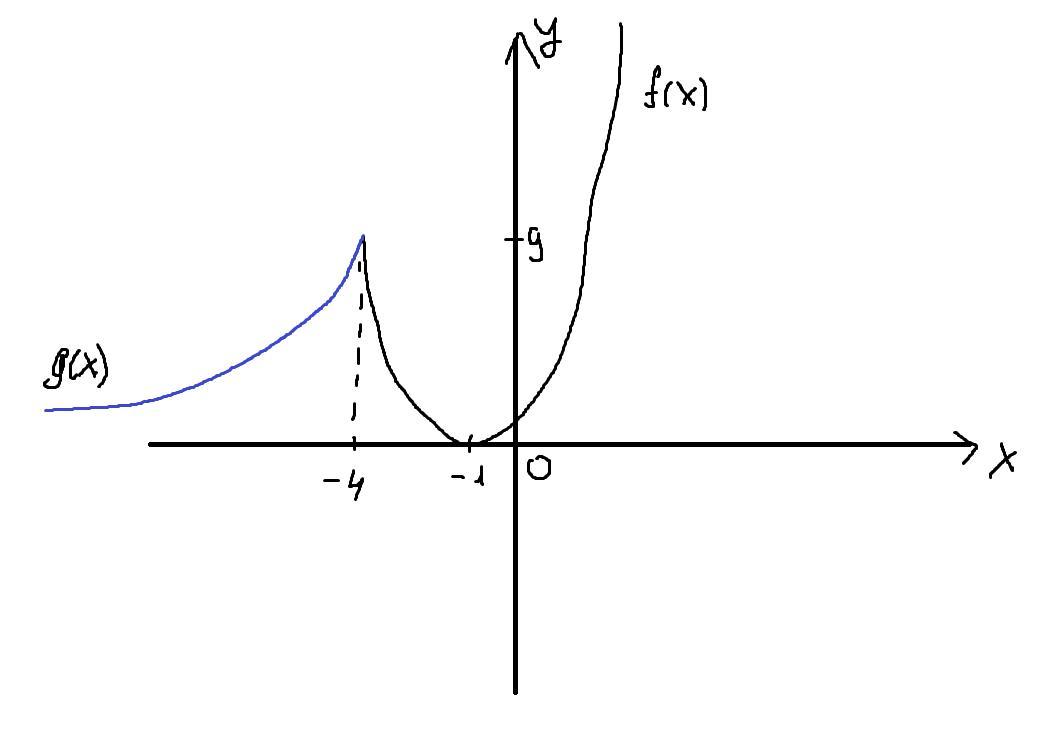
Теперь не сложно заметить,что прямая y=m имеет единственное решение при m=0 и m>9

Два решения будет при m=9

Приложения:

Irremediable: а если m = 10, то пересечения разве не будет?))

Irremediable: а.. всё верно)

maymr: Функция выделена синим?

maymr: А, всё поняла, спасибо

Новые вопросы

Математика, 1 год назад

Английский язык, 1 год назад

Математика, 1 год назад

Химия, 1 год назад

Алгебра, 6 лет назад

Математика, 6 лет назад