Постройте фигуру и вычислите её площадь, если фигура ограниченна линиями.

Ответы на вопрос
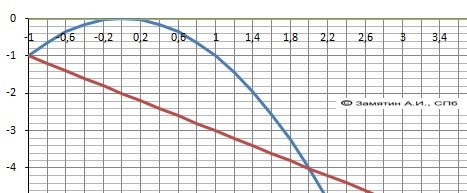
ДАНО: y(x) = - x², f(x) = -x - 2
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
1. Графики функций на рисунке в приложении.
2. Находим пределы интегрирования решив уравнение: - x² = - x - 2, a = 2 - верхний, b = -1 - нижний предел.
3. Пишем уравнение разности функций - парабола выше прямой.
s(x) = 2 + x - x² - первообразная функция.
4. S(x) = 2*x + 1/2*x² - 1/3*x³ - интеграл - площадь
5. Вычисляем. S(2) = 4 + 2 - 2 2/3 = 3 1/3 и S(-1) = -2 + 0.5 - 1/3 = - 1 1/6
Окончательно: S = 3 1/3 + 1 1/6 = 4 1/2 = 4.5 - площадь - ОТВЕТ
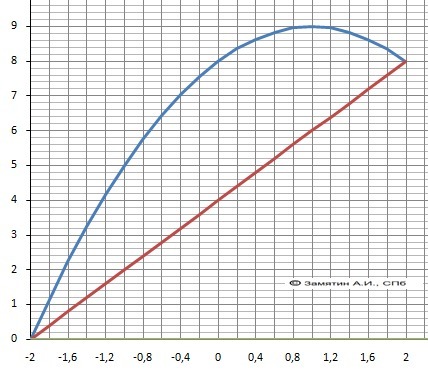
ДАНО: y(x) = - x² + 2*x + 8, f(x) = -2*x 4
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
1. Графики функций на рисунке в приложении.
2. Находим пределы интегрирования решив уравнение: x² - 4 =0,
a = 2 - верхний, b = -2 - нижний предел.
3. Пишем уравнение разности функций - парабола выше прямой.
s(x) = 4 - x² - первообразная функция.
4. S(x) = 4*x - 1/3*x³ - интеграл - площадь
5. Вычисляем. S(2) = 8 - 2 2/3 = 5 1/3 и S(-2) = -8 - 2 2/3 = - 5 1/3
Окончательно: S = 5 1/3 + 5 1/3 = 10 2/3 - площадь - ОТВЕТ (≈10.667)