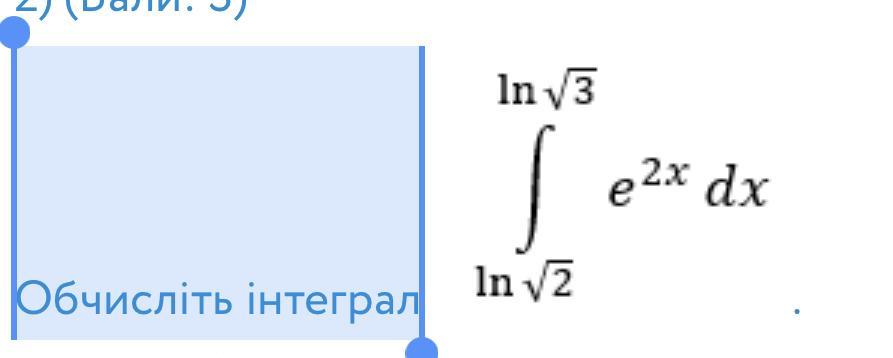
Алгебра, вопрос задал maybl9 , 11 месяцев назад

Поможіть срочно!! Обчисліть інтеграл
Бажано написати на листку

Приложения:

Simba2017: ответ 1/2

Ответы на вопрос

Ответил NNNLLL54

0

Ответ:

Вычислить определённый интеграл . Применяем формулу Ньютона-Лейбница .

$\bf \displaystyle \int\limits_{ln\sqrt2}^{ln\sqrt3}\, e^{2x}\, dx=\frac{1}{2}\int\limits_{ln\sqrt2}^{ln\sqrt3}\, e^{2x}\cdot d(2x)=\frac{1}{2}\cdot e^{2x}\, \Big|_{ln\sqrt2}^{ln\sqrt3}=\frac{1}{2}\cdot (e^{2\, ln\sqrt3}-e^{2\cdot ln\sqrt2})=\\\\\\=\frac{1}{2}\cdot (e^{ln3}-e^{ln2})=\frac{1}{2}\cdot (3-2)=\frac{1}{2}$

Приложения:

Предыдущий вопрос

Следующий вопрос

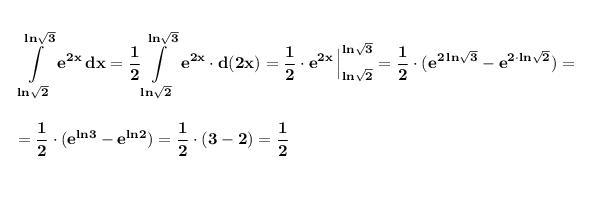
Новые вопросы

Русский язык, 8 месяцев назад

синквейн к слову сила срочно!!!

Литература, 8 месяцев назад

Какие строки не принадлежат А. С. Пушкину? "Долины сохнут и пестреют" <<От желтизны не пропадет трава» "Деревья в зимнем серебре" «Все ярко, все бело кругом»...

Английский язык, 11 месяцев назад

помогите пажалуйста очень срочно...

Оʻzbek tili, 11 месяцев назад

Ertaklar yaxshillikka yetaklar mavzusida 4 5 gapdan iborat boğlanishli matn tuzing...

Физика, 6 лет назад

Какая проводимость наблюдается в жидкостях? А) электронная, Б) ионная, В) электронно-ионная...

Английский язык, 6 лет назад

Составите вопрос. 1 общий 2 специальный My brother wento to the cinema yesterday...