ПОМОЖІТЬ ПЖПЖПЖПЖПЖЖП
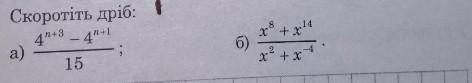
Ответы на вопрос
Ответ:
Завдання 1
[\frac{4^{n+9}-4^{n+1}}{15}]
Розкладемо числа в степені 4 на прості множники:
[4^{n+9} = (2^2)^{n+9} = 2^{2n+18}]
[4^{n+1} = (2^2)^{n+1} = 2^{2n+2}]
Тоді дріб можна перетворити так:
[\frac{2^{2n+18}-2^{2n+2}}{15} = \frac{2^{2n+2}(2^{16}-1)}{15}]
Найвищий спільний дільник чисел 2^{2n+2} і 15 дорівнює 3. Тому дріб можна скоротити на 3:
[\frac{2^{2n+2}(2^{16}-1)}{15} = \frac{2^{2n+2}}{5}\cdot\frac{2^{16}-1}{5}]
Дріб 2^{16}-1 можна скоротити на 1, оскільки 16 і 1 - взаємно прості числа. Тому отримаємо:
[\frac{2^{2n+2}}{5}\cdot\frac{2^{16}-1}{5} = \frac{2^{2n+2}}{5}\cdot 1 = \frac{2^{2n+2}}{5}]
Отже, відповідь:
[\frac{4^{n+9}-4^{n+1}}{15} = \frac{2^{2n+2}}{5}]
Завдання 2
[\frac{x^{8}+x^{14}}{x^{2}+x^{-4}}]
Розкладемо числа в степені x на прості множники:
[x^{8} = (x^2)^4 = x^{2\cdot4}]
[x^{14} = (x^2)^7 = x^{2\cdot7}]
[x^{2} = (x^2)^1 = x^{2\cdot1}]
[x^{-4} = \frac{1}{x^4} = \frac{(x^2)^2}{(x^2)^2} = x^{2\cdot-2}]
Тоді дріб можна перетворити так:
[\frac{x^{8}+x^{14}}{x^{2}+x^{-4}} = \frac{x^{2\cdot4}+x^{2\cdot7}}{x^{2\cdot1}+x^{2\cdot-2}}]
Застосуємо властивість дробу:
[\frac{x^{2\cdot4}+x^{2\cdot7}}{x^{2\cdot1}+x^{2\cdot-2}} = \frac{x^{2\cdot4}}{x^{2\cdot1}} + \frac{x^{2\cdot7}}{x^{2\cdot-2}}]
[ = \frac{x^4}{x} + \frac{x^{14}}{x^{-2}}]
[ = x^3 + x^{12}]
Отже, відповідь:
[\frac{x^{8}+x^{14}}{x^{2}+x^{-4}} = x^3 + x^{12}]
Объяснение: