Помогите( За помощь даю 30 баллов.
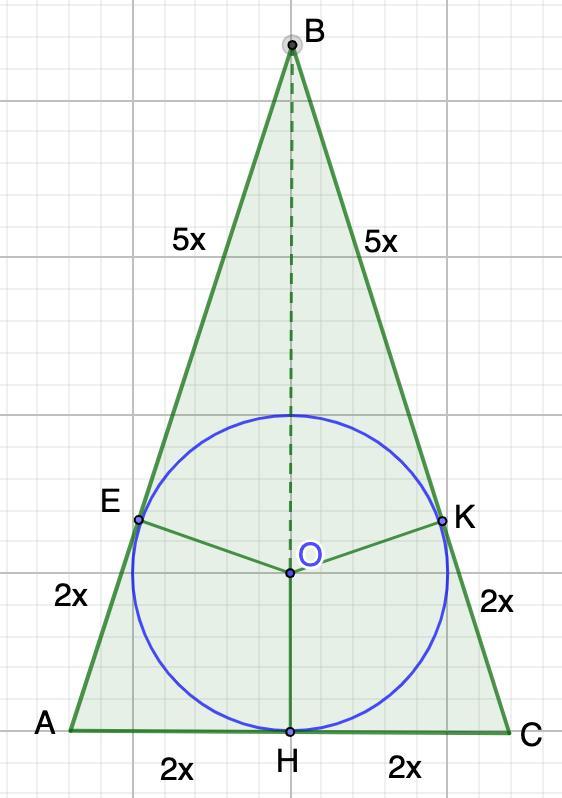
Точка дотику вписаного в рівнобедрений трикутник ABC кола ділить його бічну сторону у відношенні 5:2 ( більший відрізок прилеглий до кута, протилежного основі АС). Знайдіть сторони трикутника, якщо його периметр дорівнює 36 см.

Ответ:

Стороны треугольника равны АВ = ВС = 14 см; АС = 8 см.

Объяснение:

Точка касания вписанной в равнобедренный треугольник ABC окружности делит его боковую сторону в отношении 5:2 ( больший отрезок прилегающий к углу, противоположному основе АС). Найдите стороны треугольника, если его периметр равен 36 см.

Дано: ΔАВС - равнобедренный;

Окр.О - вписанная;

ВЕ : АЕ = 5 : 2

Р (АВС) = 36 см

Найти: стороны ΔАВС

Решение:

Рассмотрим ΔАВС - равнобедренный.

Е, К, Н - точки касания.

ВЕ : АЕ = 5 : 2

Пусть АЕ = 2х, тогда ВЕ = 5х.

• Отрезки касательных к окружности, проведенные из одной точки, равны.

⇒ ЕВ = ВК = 5х; АЕ = АН = 2х.

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ВО - биссектриса.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОН ⊥ АС.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

⇒ АН = НС = 2х

НС = СК = 2х (отрезки касательных.

• Периметр треугольника - сумма длин его сторон.

⇒ Р (АВС) = АВ + ВС + АС = (2х + 5х) + (5х + 2х) + (2х + 2х)

36 = 18х

х = 2

АВ = ВС = (2х + 5х) = 7х = 2 · 7 = 14 (см)

АС = (2х + 2х) = 4х = 2 · 4 = 8 (см)

Стороны треугольника равны АВ = ВС = 14 см; АС = 8 см.