Математика, вопрос задал vikasuhareva2001 , 6 лет назад

помогите вычислить пределы функции

Приложения:

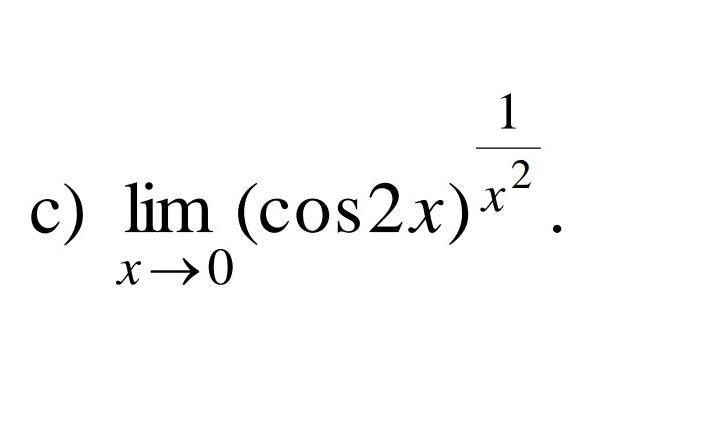
Ответы на вопрос

Ответил NNNLLL54

2

Ответ:

Для вычисления предела применим второй замечательный предел $\lim\limits_{x \to 0}\, (1+x)^{\frac{1}{x}}=e$ .

$\lim\limits_{x \to 0}\, \Big(cos2x\Big)^{\frac{1}{x^2}}=\lim\limits_{x \to 0}\, \displaystyle \Big(cos2x+1-1\Big)^{\frac{1}{x^2}}=\lim\limits_{x \to 0}\, \Big(1+(\underbrace{cos2x-1}_{\to \, 0})\Big)^{\frac{cos2x-1}{(cos2x-1)\, x^2}}=\\\\\\=\lim\limits_{x \to 0}\, \left(\Big(1+(cos2x-1)\Big)^{\frac{1}{(cos2x-1)}}\right)^{\frac{cos2x-1}{x^2}}=e^{\lim\limits_{x \to 0}\frac{cos2x-1}{x^2}}=e^{\lim\limits_{x \to 0}\frac{-(1-cos2x)}{x^2}}=$

$=e^{\lim\limits_{x \to 0}\frac{-2sin^2x}{x^2}}=e^{\lim\limits_{x \to 0}\frac{-2x^2}{x^2}}=e^{-2}=\dfrac{1}{e^2}$

В последней строчке заменили беск. малую величину $sin^2x$ на эквивалентную ей бесконечно малую величину $x^2$ при $x\to 0$ .

Ответил nikebod313

3

Решение задания во вложении.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

lmagine there is a new pupil in your class.

Окружающий мир, 1 год назад

что означает слово поросенок...

Математика, 6 лет назад

Помогите пожалуйста!!!!!!! Реши уравнения: $x \times 8 = 96$ $x \div 3 = 24$ ...

Математика, 6 лет назад

помогите пожалуйста очень нужна помощь...

Алгебра, 8 лет назад

Какие из чисел 1,2,3,-3,-2,-1 являются корнями уравнения x2+2x2-2=10...

Математика, 8 лет назад

Реши задачу. Вычисли и запиши ответ. Два поезда одновременно отправились от одной станции в протевоположных направлениях. Через 2ч расстояние между ними стало 280км.С какой средней скоростью двигался...