Алгебра, вопрос задал Rendon1 , 2 года назад

Помогите вычислить определенный интеграл

$\int\limits^0_{-2} (4-3x)*e^{-3x} } dx$

Ответы на вопрос

Ответил tracv9175

Ответ:

-1+3е⁶.

Объяснение:

Приложения:

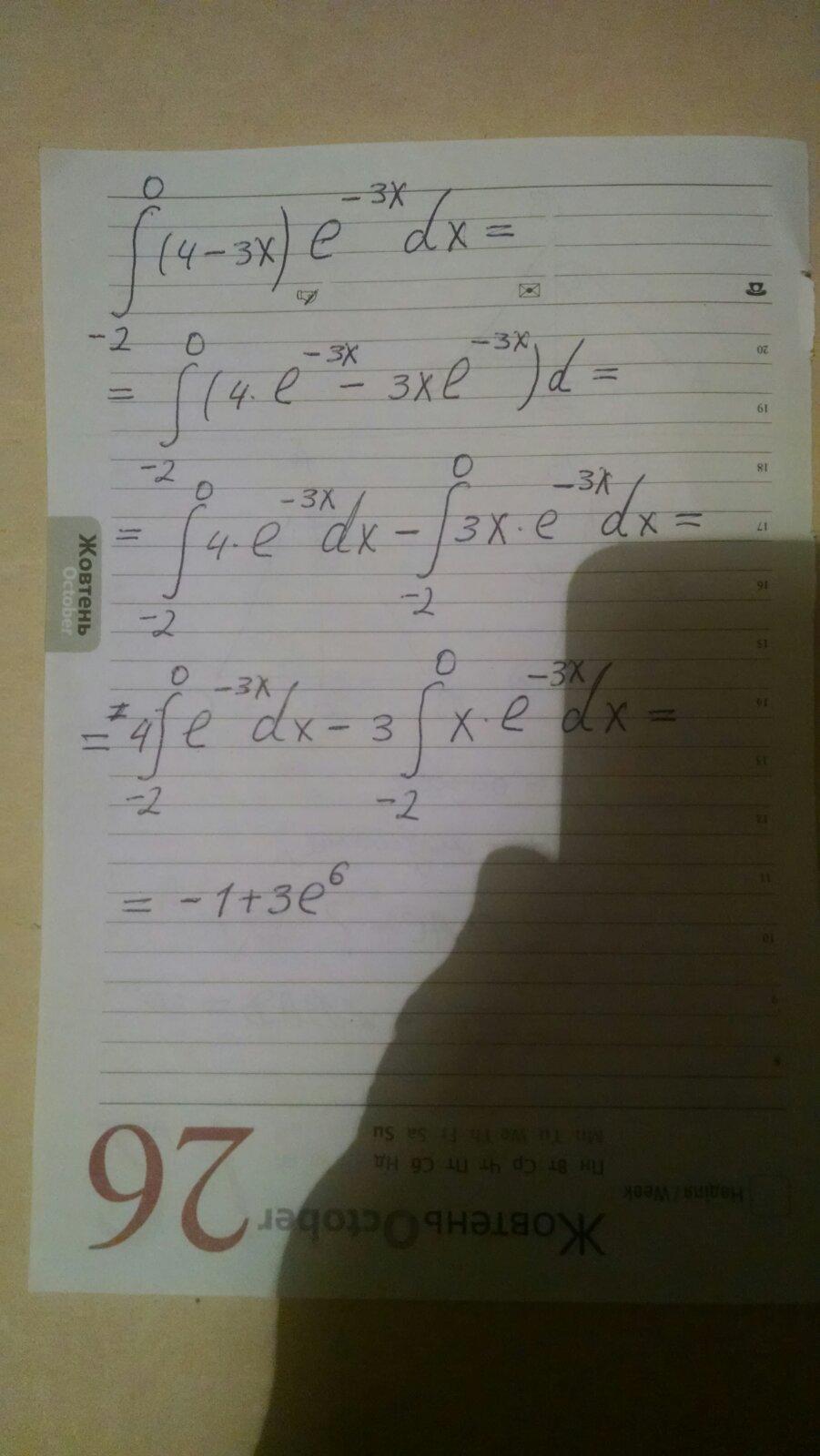
NNNLLL54: разбивать на 2 интеграла не обязательно

Ответил NNNLLL54

Ответ:

$\int\limits^0_{-2}\, (4-3x)\cdot e^{-3x}\, dx=\Big[\ u=4-3x\ ,\ du=-3\, dx\ ,\ dv=e^{-3x}\, dx\ ,\\\\\\v=-\dfrac{1}{3}\, e^{-3x}\ ,\ \ \int u\, dv=uv-\int v\, du\ \Big]=-\dfrac{1}{3}\cdot (4-3x)e^{-3x}\, \Big|_{-2}^0-\dfrac{3}{3}\int \limits _{-2}^0e^{-3x}\, dx=\\\\\\=-\dfrac{1}{3}\cdot (4-10e^6)+\dfrac{1}{3}\, e^{-3x}\, \Big|_{-2}^0= -\dfrac{1}{3}\cdot (4-10e^6)+\dfrac{1}{3}\cdot (1-e^6)=\\\\\\=-\dfrac{4}{3}+\dfrac{10}{3}\, e^6+\dfrac{1}{3}-\dfrac{1}{3}\, e^6=-1+3e^6=3e^6-1$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

выпиши из ,,Ночь перед рождестовом" 6 слов с суффиксами ЩИК и ЧИК. Помогите пожалуйста.

Английский язык, 1 год назад

Answer the questions about you. Did you go to school yesterday?

Математика, 2 года назад

Запиши величины 11т,1.100кг,110т,110кг,110г в порядке их возрастания...

Математика, 2 года назад

Решите Уравнения Линейные с одной переменной ...

География, 7 лет назад

размыв горных пород, почв текущей водой называется: 1) Аккумуляция 2) Эрозия 3) Падение реки...

Математика, 7 лет назад

Докажите что функция f(x) является четной, а функция g(x) нечётной...