Помогите!!
В кінці відрізка завдовжки 6 см належать двом перпендикулярним площинам і віддалені від прямої перетини цих площин на 3 см і 5√2. Відповідно. Знайдіть кути що утворює відрізок із заданими площинами

Ответ:

Искомые углы равны 30° и 45°.

Объяснение:

В условии задачи явная опечатка: катет, равный 5√2 ≈ 7 см больше гипотенузы (наклонная = 6 см).

Примем условие с расстояниями от концов отрезка до линии пересечения перпендикулярных плоскостей равными 3 см и 3√2 см.

Решение.

Угол между наклонной и плоскостью - это угол между наклонной и проекцией этой наклонной на плоскости.

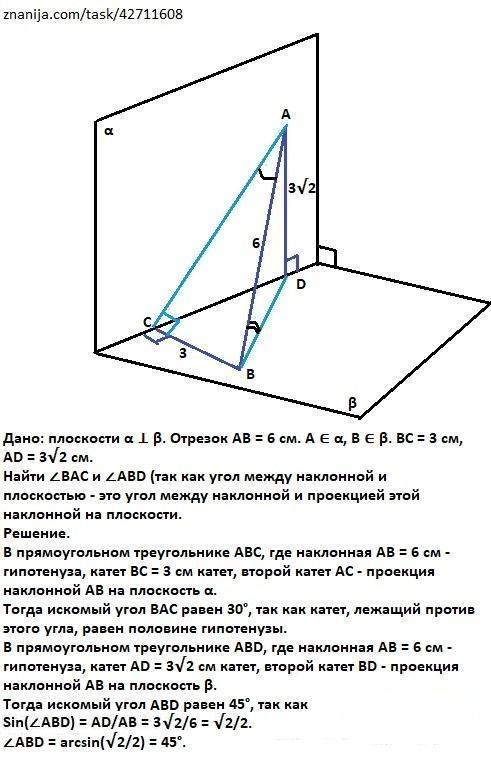
В нашем случае плоскости α ⊥ β. Отрезок АВ = 6 см.

А ∈ α, В ∈ β. ВС = 3 см, AD = 3√2 см.

Найти ∠ВАС и ∠АВD.

В прямоугольном треугольнике АВС, где наклонная АВ = 6 см - гипотенуза, катет ВС = 3 см катет, второй катет АС - проекция наклонной АВ на плоскость α.

Тогда искомый угол ВАС равен 30°, так как катет, лежащий против этого угла, равен половине гипотенузы.

В прямоугольном треугольнике АВD, где наклонная АВ = 6 см - гипотенуза, катет AD = 3√2 см катет, второй катет BD - проекция наклонной АВ на плоскость β.

Тогда искомый угол АВD равен 45°, так как

Sin(∠ABD) = AD/AB = 3√2/6 = √2/2.

∠ABD = arcsin(√2/2) = 45°.