ПОМОГИТЕ СРОЧНО РЕШИТЬ!!
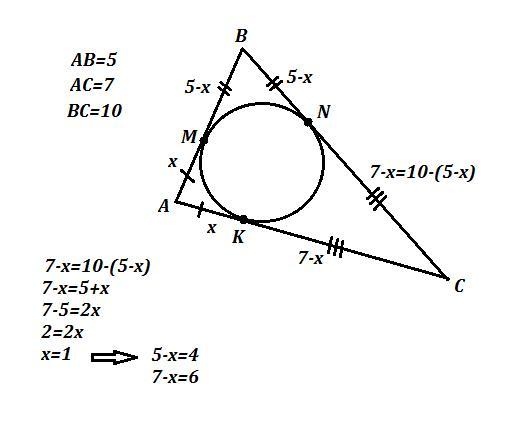
Стороны треугольника равны 5см. 7см и 10см. Найдите отрезки, на которые точка касания вписаной отружности делит наибольшую сторону.

Ответ:  6 и 4 .

Объяснение:

AB=5 , BC=10 , AC=7

Наибольшая сторона - ВС=10.

Стороны треугольника, в который вписана окружность, являются для окружности касательными. А отрезки касательных, проведённых к окружности из одной точки, равны.

Точки касания вписанной окружности сторон треугольника обозначим через М , N , K . А также обозначим через х отрезок АМ, тогда  АM=АК=х , ВМ=5-x=BN , CK=7-x=CN=10-(5-x).

7-x=10-(5-x)

7-x=5+x

2x=2

x=1   ⇒   CN=7-1=6 ,  BN=5-1=4