Математика, вопрос задал annaelgina8947 , 2 года назад

Помогите срочно решить +10 монет

Приложения:

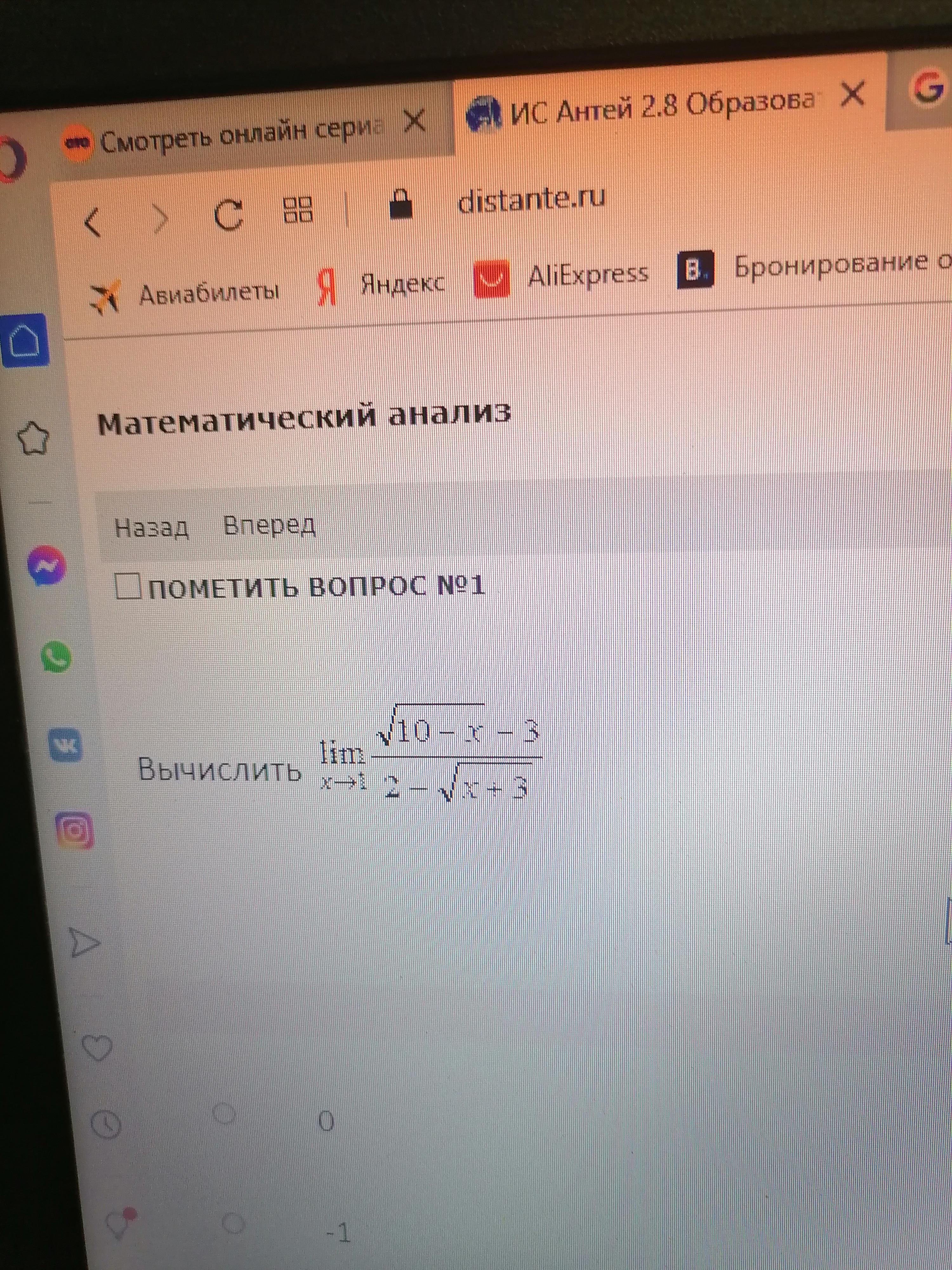
Ответы на вопрос

Ответил pushpull

Ответ:

Пошаговое объяснение:

здесь можно решать двумя способами

либо домножать числите и знаменатель сначала на √(10-х) +3

потом на -2 -√(х+3)

и в результате получить предел

$\lim_{x \to \Х1} \frac{2+\sqrt{x+3} }{3+\sqrt{10-x} }=\frac{2}{3}$

но с этим много возни с дробями и это не рационально.

либо применить правило Лопиталя и брать производные от числителя и знаменателя до тех пор, пока не избавимся от неопределенности.

у нас видно, что производную придется брать только 1 раз

так и поступим.

$(\sqrt{10-x}-3)' = -\frac{1}{2\sqrt{10-x} } \\\\(2-\sqrt{x+3} )' = -\frac{1}{2\sqrt{x+3} }$

теперь получим наш предел

$( -\frac{1}{2\sqrt{10-x} }) : ( -\frac{1}{2\sqrt{x+3} } )= \frac{\sqrt{x+3} }{\sqrt{10-x} }$

$\lim_{x \to \Х1} \frac{\sqrt{x+3} }{\sqrt{10-x} }=\frac{2}{3}$

annaelgina8947: спасибо

pushpull: пожалуйста. успехов -))

Новые вопросы

Русский язык, 1 год назад

Українська мова, 1 год назад

Английский язык, 2 года назад

Литература, 2 года назад

Литература, 7 лет назад

Литература, 7 лет назад