Помогите срочно, пожалуйста

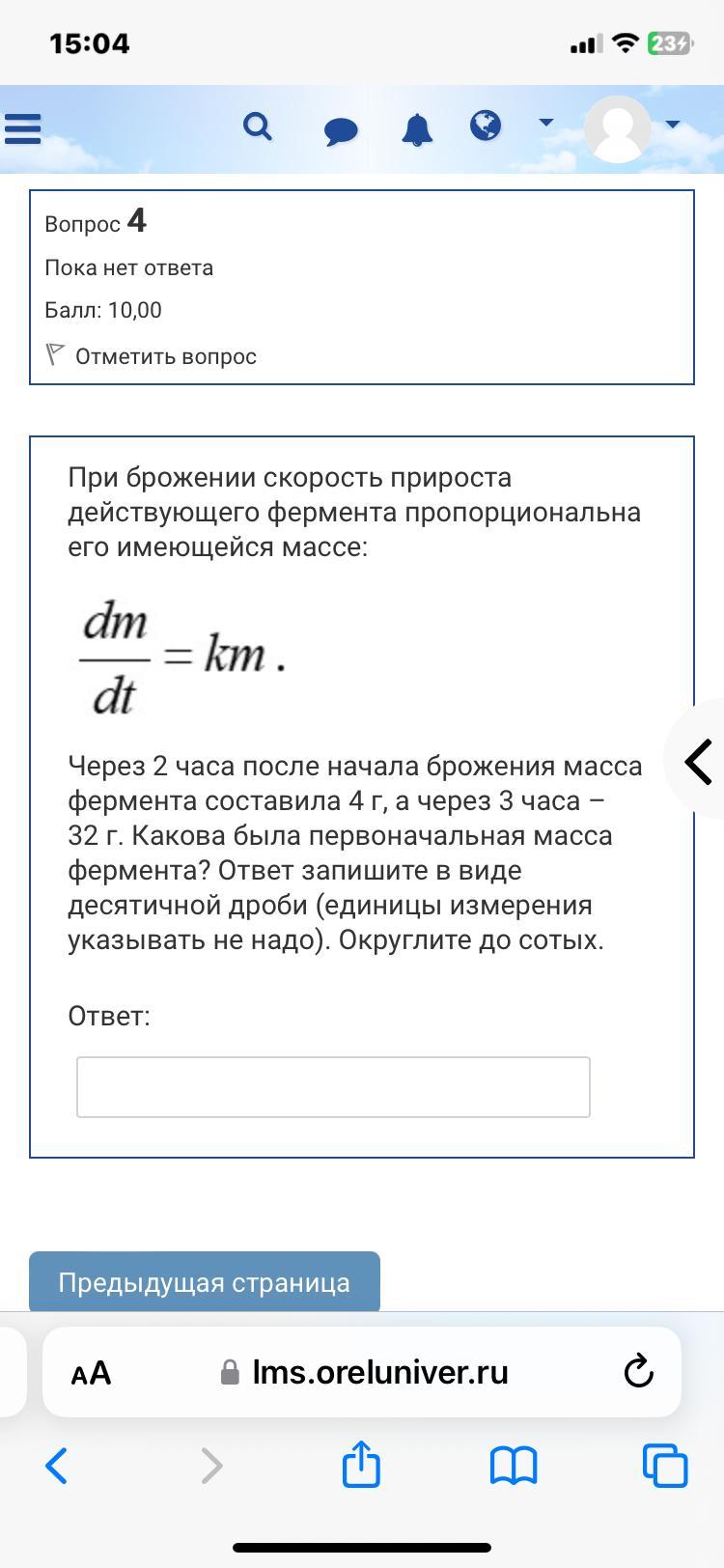
Дано дифференциальное уравнение роста массы фермента:

\(\frac{dm}{dt} = km\).

Решение этого уравнения имеет вид: \(m(t) = Ce^{kt}\), где \(C\) - постоянная интегрирования.

Подставим значения времени \(t = 2\) часа и \(t = 3\) часа:

1. При \(t = 2\), \(m(2) = Ce^{2k} = 4\).
2. При \(t = 3\), \(m(3) = Ce^{3k} = 32\).

Разделим уравнения:

\(\frac{Ce^{3k}}{Ce^{2k}} = \frac{32}{4}.\)

Упростим:

\(e^k = 8.\)

Теперь, чтобы найти начальную массу (\(C\)), подставим \(t = 0\), так как \(e^0 = 1\):

\(m(0) = Ce^{0} = C = ?\)

Таким образом, начальная масса фермента (\(C\)) равна 1 г.

Ответ: 1 г.