Помогите срочно пожалуйста
Приложения:
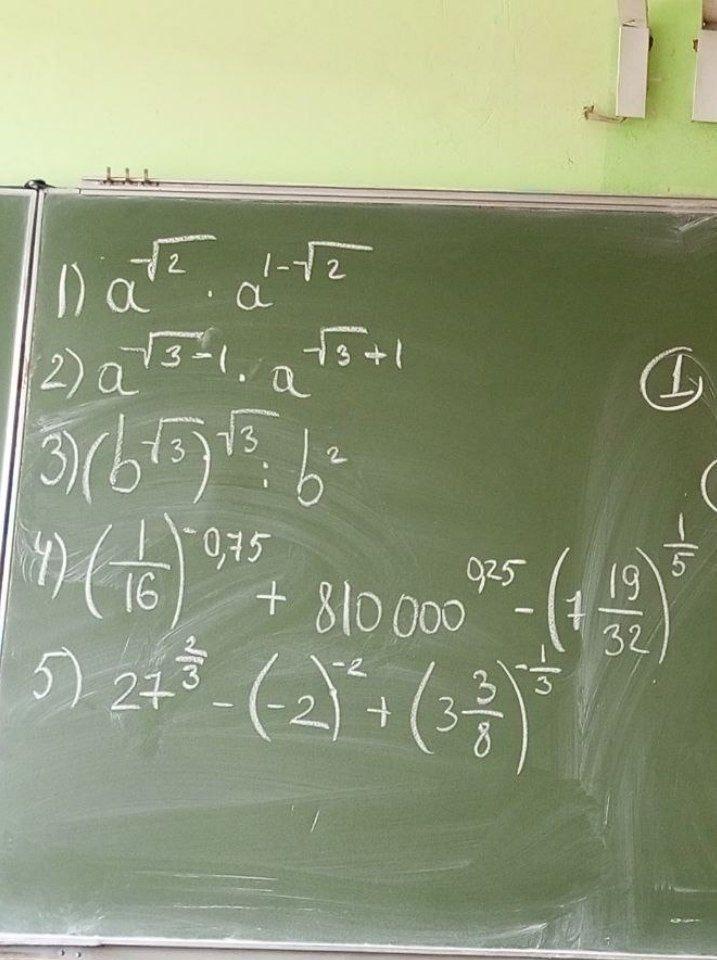
Ответы на вопрос
Ответил NNNLLL54
0
Ответ:
Упростить выражения . Применяем свойства степеней .
Приложения:

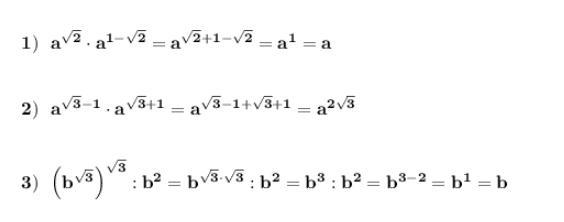
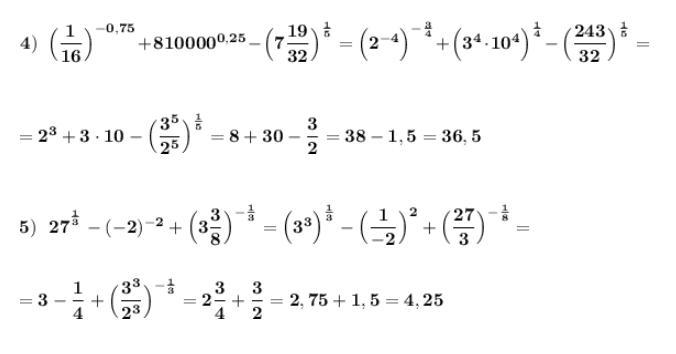
Новые вопросы
Математика,
11 месяцев назад
Математика,
11 месяцев назад
Информатика,
1 год назад
Другие предметы,
1 год назад
Українська література,
6 лет назад