ПОМОГИТЕ СРОЧНО!!!
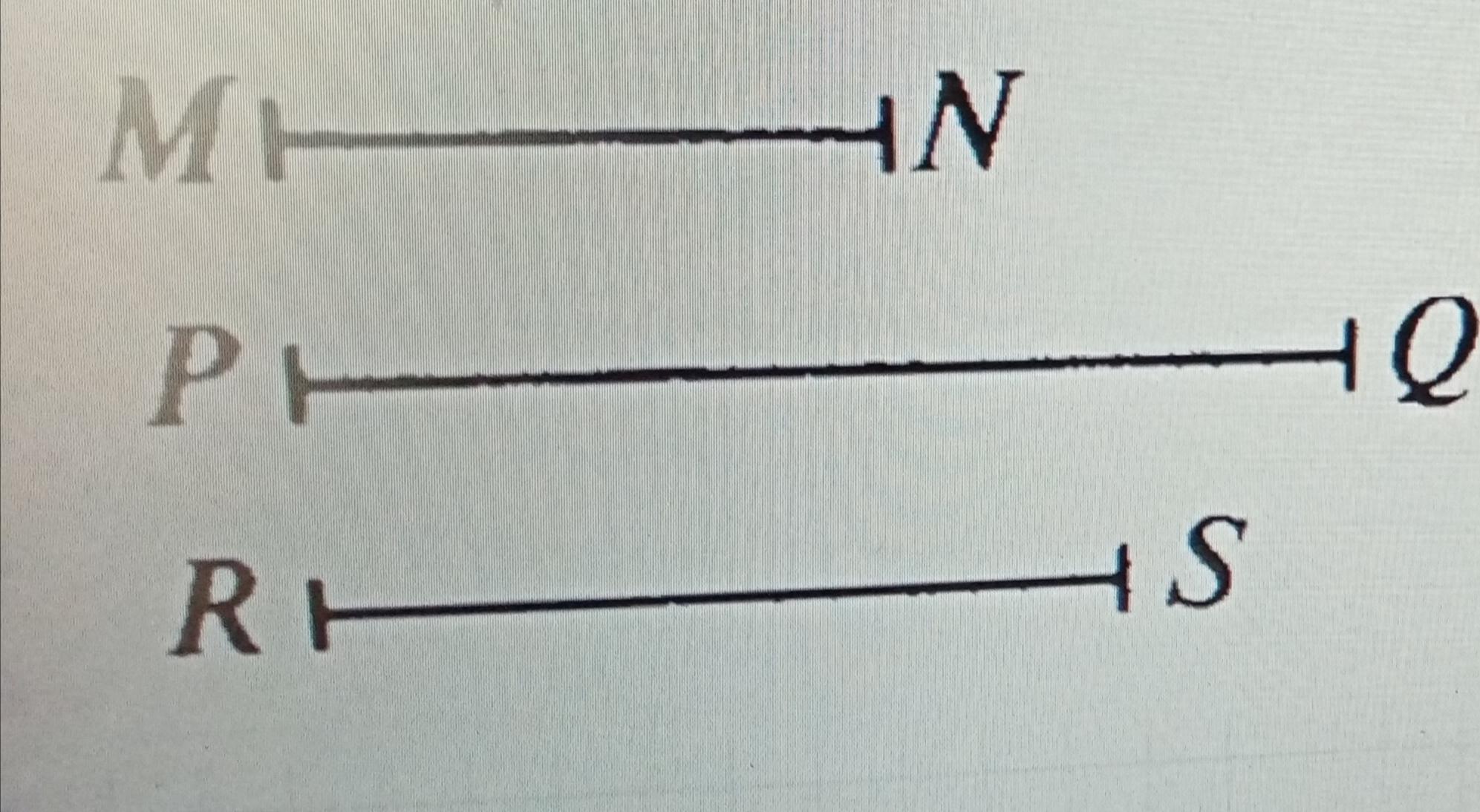
Построить :треугольник ABC такой, что AB=MN, BC=PQ, AC=RS, с помощью циркуля и линейки
Рисунок к задаче прикреплён

Даны отрезки MN, PQ, RS, равные сторонам искомого треугольника, причём AB=MN, BC=PQ, AC=RS.

Необходимо построить треугольник АВС со сторонами, равными данным отрезкам.

Задача на построение - это задача, в которой надо построить геометрический объект, пользуясь только двумя инструментами: линейкой и циркулем.

В случае построения треугольника по трём сторонам необходимо убедиться, что исполняется неравенство треугольника: длина каждого отрезка должна быть меньше суммы длин двух других отрезков.

Если это условие выполняется (в нашем случае -да), то:

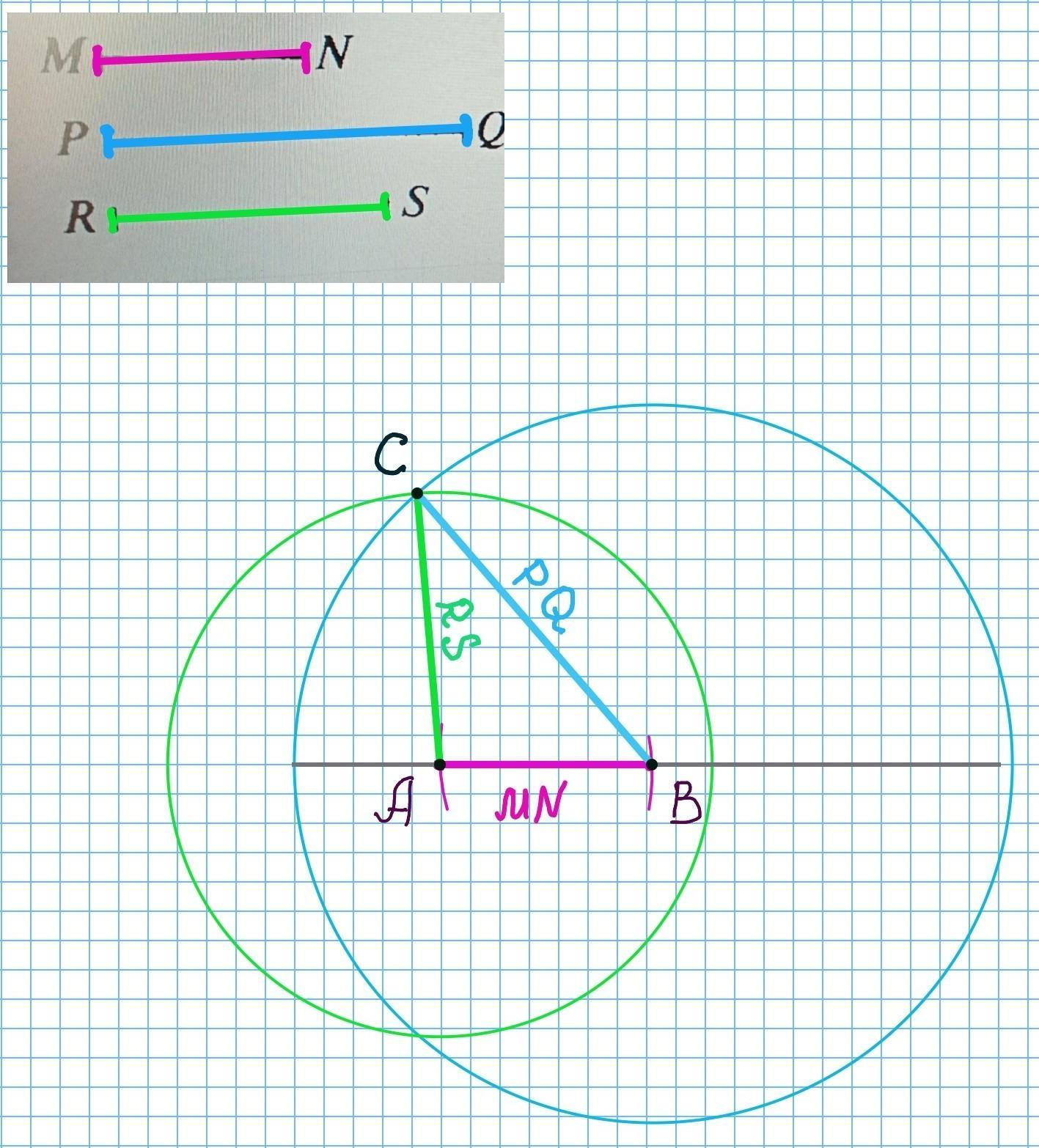
1. Проведём прямую (серая линия)
2. На прямой отметим точку А. От неё отложим отрезок АВ=MN (розовая линия). Это можно сделать как линейкой, так и циркулем. Точка В - другой конец отрезка.
3. Проведём окружность с центром в точке А и радиусом, равным отрезку RS (зелёная окружность).
4. Проведём окружность с центром в точке В и радиусом, равным отрезку PQ (голубая окружность).
5. С- точка пересечения окружностей. Она является третьей вершиной треугольника. (Как мы видим на рисунке, у нас две точки пересечения окружностей. Можно выбрать любую из них.)
6. Соединив точки А,С (зелёная линия) и В,С (голубая линия) получим искомый треугольник.

Построенный треугольник - искомый. Он равен всем треугольникам, которые имеют данные нам стороны по трём сторонам ( третий признак равенства треугольников).