Алгебра, вопрос задал danaigor277 , 2 года назад

Помогите срочно нужно решить уровнение до завтра​

Приложения:

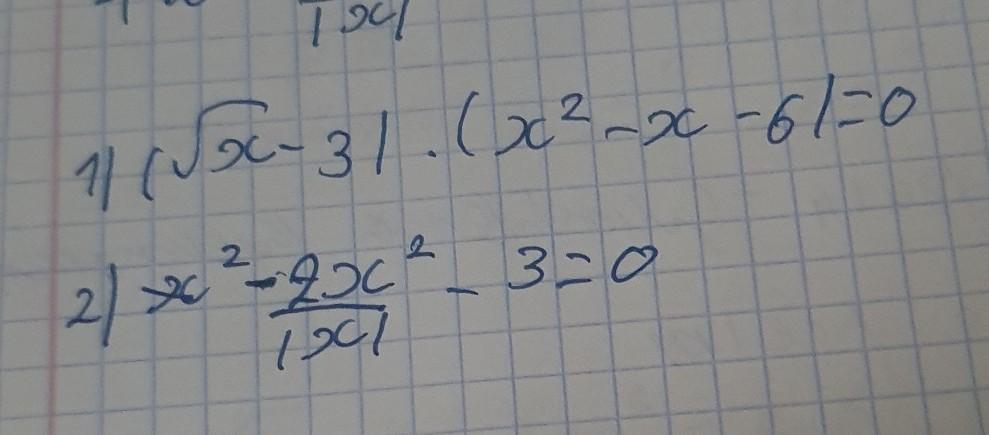
Ответы на вопрос

Ответил yevheniiavz
1

....................................

Приложения:
danaigor277: Огромное тебе спасибо
BMW52: В1) должна быть совокупность. Во 2) нет пояснения отбора корней.
Ответил NNNLLL54
1

Ответ:

1)\ \ (\sqrt{x}-3)(x^2-x-6)=0    ,       ООФ:  x\geq 0  .

Произведение равно 0 , если хотя бы один из множителей равен 0 .

a)\ \ \sqrt{x} -3=0\ \ \Rightarrow \ \ \ \sqrt{x}=3\ \ ,\ \ \underline{x=9} > 0\\\\b)\ \ x^2-x-6=0\ \ ,\\\\teorema\ Vieta:x_1+x_2=1\ \ ,\ \ x_1\cdot x_2=-6\ \ \Rightarrow \\\\x_1=-2 < 0\ \ \ ,\ \ \ \underline{x_2=3} > 0  

Значения переменной  х  должны быть неотрицательны, поэтому  

х= -2  не подходит .

Ответ:  x=9  или  x=3\ .

2)\ \ x^2-\dfrac{2x^2}{|x|}-3=0  

ООФ:   |x|\ne 0\ \ \ \Rightarrow \ \ \ x\ne 0  

Рассмотрим 2 случая: когда  х>0  и когда  x<0 .

a)\ \ x &gt; 0\ \ \Rightarrow \ \ \ |x|=x\\\\x^2-\dfrac{2x^2}{x}-3=0\ \ ,\ \ \ x^2-2x-3=0\ \ ,\ \ x_1=-1\ ,\ x_2=3\ (teorema\ Vieta)  

Так как рассматриваем случай при  x>0 , то х= -1  не подходит .

b)\ \ x &lt; 0\ \ \Rightarrow \ \ \ |x|=-x\\\\x^2-\dfrac{2x^2}{-x}-3=0\ \ ,\ \ x^2+2x-3=0\ \ ,\ \ x_1=-3\ ,\ x_2=1\ (teorema\ Vieta)

Так как рассматриваем случай при   x<0 , то х=1  не подходит .

Ответ:  x = 3  ,  x = -3 .

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Английский язык, 1 год назад
Помогите перевести на английский слово: аллея...
Русский язык, 1 год назад
Определи способ образования слов. Распредели сложные слова по группам, в зависимости от того, что соединяется при их образовании: 1) слова, 2)основы слов, 3) начальная часть слова и целое слово, 4)...
Українська мова, 2 года назад
З’ясуйте тип складного речення.
Математика, 2 года назад
знайти границю функції. lim x→∞ (2x)/(2x+1)^x​...
Математика, 7 лет назад
на палубе корабля было 12 моряков. Это на 2 моряков больше,чем было в каютах.Сколько всего моряков было на палубе и в каютах?
Математика, 7 лет назад
У небольшого аквариума высота и ширина приблизительно равны,а длинна превышает высоту в два раза.аквариум среднего размера имеет длинну около 800мм.доя конструирования аквариума нужно пять стёкол:два...