помогите срочно надо!!!!!!! найдите наибольшее и наименьшее значение функции : у=1/3 х^3-x^2+1 на отрезке (-1;3)
Ответы на вопрос
Ответил dnepr1
1
Требуется найти критические точки функции, которые определяются производной, приравненной к 0:
y' = x²-2x = х(х-2) = 0.
Отсюда 2 корня: х₁ = 0
х₂ = 2.
Теперь надо определить, где минимум, а где максимум,
Если при прохождении через критическую точку производная меняет знак с минуса на плюс, то есть это будет минимум, а если меняет знак с плюса на минус, соответственно это будет максимум.
Найдём значения производной при х = -1 и х = 1
х = -1 y' = (-1)²-2*(-1) = 1+2 = 3.
x = 1 y' = 1²-2*1 = 1-2 = -1.
Знак меняется с + на - (это максимум).
Так же надо поступить и с второй точкой.
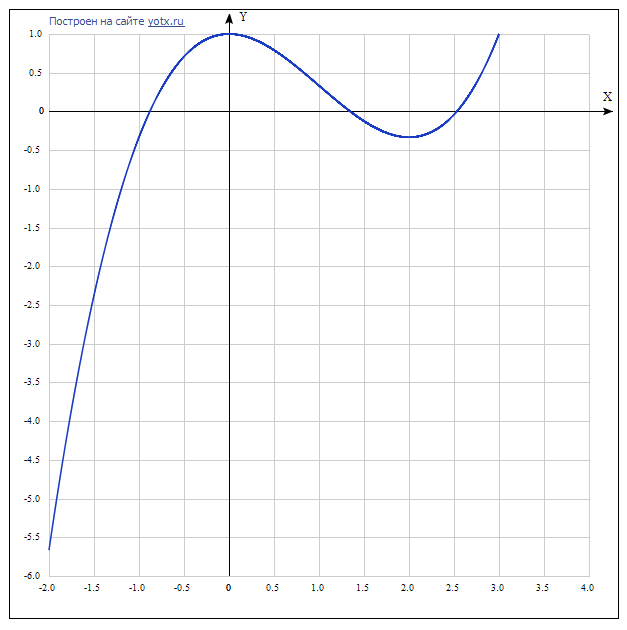
В приложении даётся график для наглядности определения точек.
y' = x²-2x = х(х-2) = 0.
Отсюда 2 корня: х₁ = 0
х₂ = 2.
Теперь надо определить, где минимум, а где максимум,
Если при прохождении через критическую точку производная меняет знак с минуса на плюс, то есть это будет минимум, а если меняет знак с плюса на минус, соответственно это будет максимум.
Найдём значения производной при х = -1 и х = 1
х = -1 y' = (-1)²-2*(-1) = 1+2 = 3.
x = 1 y' = 1²-2*1 = 1-2 = -1.
Знак меняется с + на - (это максимум).
Так же надо поступить и с второй точкой.
В приложении даётся график для наглядности определения точек.
Приложения:
tuktarovaglash2:
а откуду вы взяли х=1?
Это взяты 2 точки слева и справа от критической точки для определения знака и, соответственно, характера экстремума (смотри в ответе пояснение).
а эти точки же надо в функцию подставлять, а не в производную?
Нет, характер точки определяет производная.
Новые вопросы