Помогите срочно,хотя б меньше половины,благодарствую)
Приложения:

Ответы на вопрос
Ответил ГлупаяАнимешница
0
Я не смогла делать один пример...Простите
Приложения:
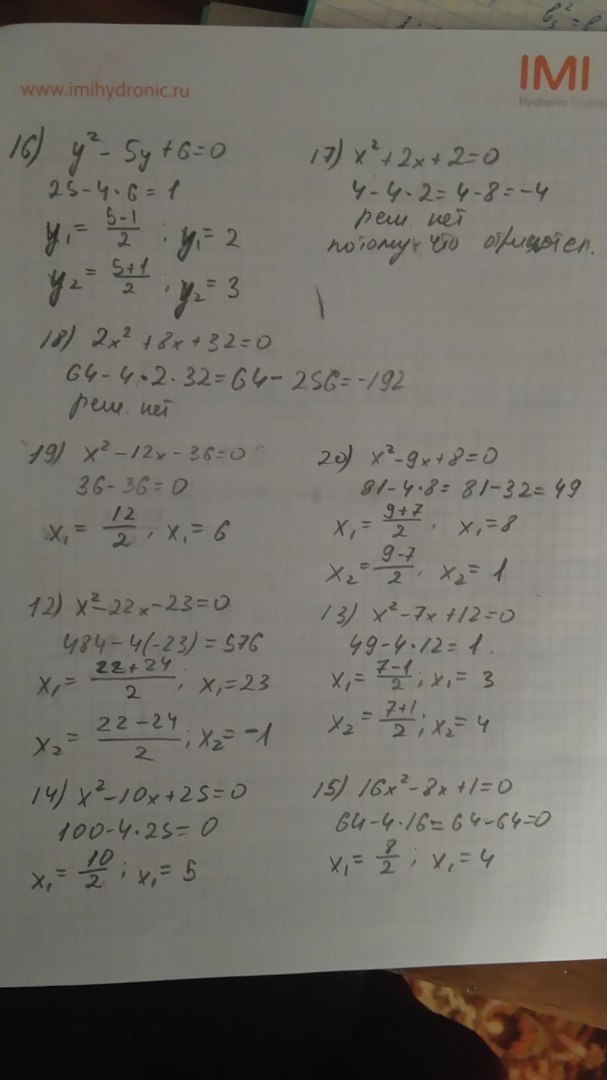

Ответил NikKurllz
0
Спасибо огромное,выручили<3
Ответил Аноним
0
Думаю дискриминанты и четвертьдискриминанты все знают а о Т. Виета хотя бы слышали
она гласит: "если х₁ и х₂ - корни ax² + bx +c то х₁ · х₂ =с /a х₁ + х₂ = -b /a
На практике: перебираем множители с·а = множ₁ · множ₂
чтобы множ₁ + множ₂ = -b
x₁ = множ₁/a
x₂ = множ₂/a
11) x² + 6x - 19 = 0
19 = 19·1 целых корней нет
D/4 = 9 + 19 = 28

12) x² - 22x - 23 = 0
23 = 23·1 (если c минусом то у меньшего корня ставится знак перед b)
c минусом то у меньшего корня ставится знак перед b)

13) x² - 7x + 12 = 0
12 = 12·1 = 3·4

14) x² - 10x + 25 = 0
25 = 25·1 = 5·5
x = 5
15) 16x² - 8x + 1 = 0
16 = 16·1 = 4·4

16) y² - 5y + 6 = 0
6 = 6·1 = 3·2

17) x² + 2x + 2 = 0
2 = 2·1 целых корней нет
D₁ = 1 - 2 < 0
18) 2x² + 8x + 32 = 0
x² + 4x + 16 = 0
16 = 16·1 = 4·4
x = - 4
19) x² - 12x = 36 = 0 (забыли Shift)
x² - 12x + 36 = 0
36 = 36·1 = 18·2 = 6·6
x = 6
20) x² - 9x + 8 = 0
8 = 8·1

1)

2) 0,2 - 2(x + 1)=0,4x
0,2 - 2x - 2 - 0,4x = 0
-2,4x - 1,8 = 0 | :6 ·(-10)
| :6 ·(-10)
4x + 3 = 0
x = -0,75
3) x² + 6x = 0

4) 2x² - 8 = 0
x² - 4= 0

5) 3x² + 2x - 5 = 0
15 = 15·1 = 5·3 (перед меньшим плюс)

6) 3x² + 9x = 12x -x²
4x² - 3x= 0
x(4x - 3) = 0

7) (5x - 4)(x + 8) = 0

8)

она гласит: "если х₁ и х₂ - корни ax² + bx +c то х₁ · х₂ =с /a х₁ + х₂ = -b /a
На практике: перебираем множители с·а = множ₁ · множ₂
чтобы множ₁ + множ₂ = -b
x₁ = множ₁/a
x₂ = множ₂/a
11) x² + 6x - 19 = 0
19 = 19·1 целых корней нет
D/4 = 9 + 19 = 28
12) x² - 22x - 23 = 0
23 = 23·1 (если
13) x² - 7x + 12 = 0
12 = 12·1 = 3·4
14) x² - 10x + 25 = 0
25 = 25·1 = 5·5
x = 5
15) 16x² - 8x + 1 = 0
16 = 16·1 = 4·4
16) y² - 5y + 6 = 0
6 = 6·1 = 3·2
17) x² + 2x + 2 = 0
2 = 2·1 целых корней нет
D₁ = 1 - 2 < 0
18) 2x² + 8x + 32 = 0
x² + 4x + 16 = 0
16 = 16·1 = 4·4
x = - 4
19) x² - 12x = 36 = 0 (забыли Shift)
x² - 12x + 36 = 0
36 = 36·1 = 18·2 = 6·6
x = 6
20) x² - 9x + 8 = 0
8 = 8·1
1)
2) 0,2 - 2(x + 1)=0,4x
0,2 - 2x - 2 - 0,4x = 0
-2,4x - 1,8 = 0
4x + 3 = 0
x = -0,75
3) x² + 6x = 0
4) 2x² - 8 = 0
x² - 4= 0
5) 3x² + 2x - 5 = 0
15 = 15·1 = 5·3 (перед меньшим плюс)
6) 3x² + 9x = 12x -x²
4x² - 3x= 0
x(4x - 3) = 0
7) (5x - 4)(x + 8) = 0
8)
Приложения:
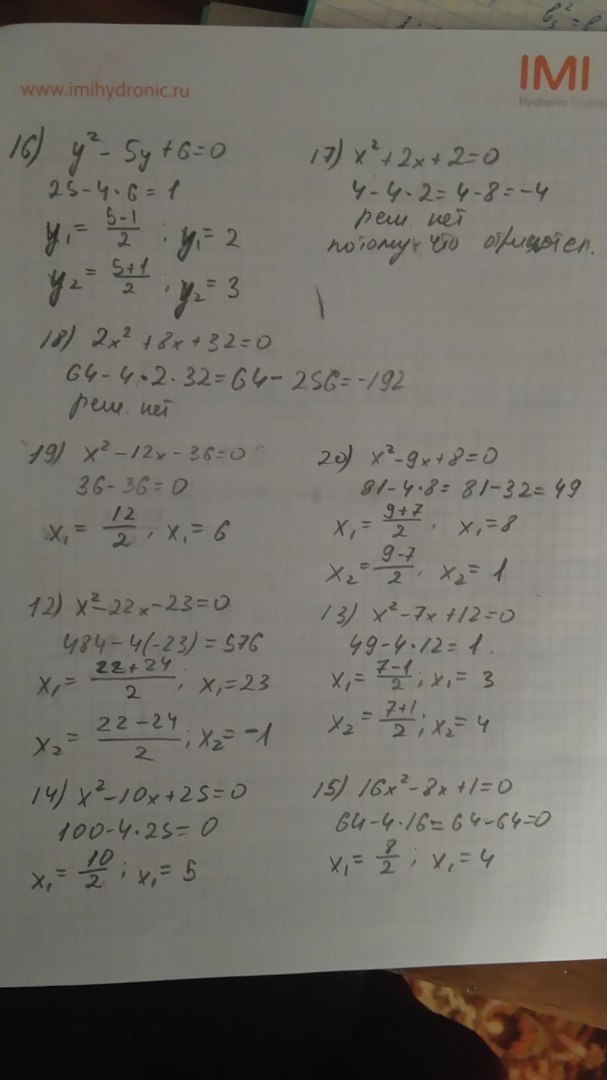

Новые вопросы
Русский язык,
2 года назад
ОБЖ,
2 года назад
Физика,
8 лет назад
География,
8 лет назад
Математика,
9 лет назад