Алгебра, вопрос задал Kolokokosik , 2 года назад

ПОМОГИТЕ! СРОЧНО! Даю 100 баллов
Упростить выражение

Приложения:

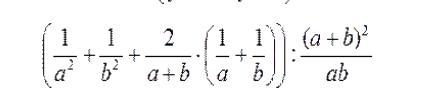
Ответы на вопрос

Ответил mathkot

2

Ответ:

$\boldsymbol{ \boxed{ \displaystyle \Bigg( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{2}{a + b} \cdot \bigg( \frac{1}{a} + \frac{1}{b} \bigg) \Bigg) :\frac{(a + b)^{2}}{ab} = \frac{1}{ab} }}$

Примечание:

Формула сокращенного умножения:

$\boxed{a^{2} + 2ab + b^{2} = (a + b)^{2}}$

Приведение дроби к общему знаменателю:

$\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd}$

Объяснение:

$\displaystyle \Bigg( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{2}{a + b} \cdot \bigg( \frac{1}{a} + \frac{1}{b} \bigg) \Bigg) :\frac{(a + b)^{2}}{ab} =$

$= \displaystyle \frac{ab}{(a + b)^{2}} \Bigg( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{2}{a + b} \cdot \bigg( \frac{a + b}{ab} \bigg) \Bigg) = \frac{ab}{(a + b)^{2}} \Bigg( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{2}{a + b} \cdot \frac{a + b}{ab} \Bigg)=$

$\displaystyle = \frac{ab}{(a + b)^{2}} \Bigg( \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{2}{ab} \Bigg)= \frac{ab}{(a + b)^{2}} \Bigg( \frac{a^{2} + b^{2}+2ab}{a^{2}b^{2}} \Bigg)= \frac{ab}{(a + b)^{2}} \cdot \frac{(a + b)^{2}}{(ab)^{2}} =$

$= \dfrac{1}{ab}$

Kolokokosik: Благодарствую

vahilovdmi: Здравствуйте, не могли бы вы мне помочь с вопросом?

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

словарный диктант укажи род имен существительных Вставь пропущенные буквы...

Русский язык, 1 год назад

Составить диалог в котором обсудите поступок мальчиков симулянтов про поступок мальчиков симулянтов в классе...

Математика, 2 года назад

40.) Найдите: 1) 10% от 35 кг; от 80 м; от 100 л. 2) 25% от 16 кг; от 84 м; от 120 л.

Биология, 2 года назад

Звідки організми беруть енергію для здійснення росту і розвитку...

Биология, 7 лет назад

Докажите, что слизь, покрывающая тело лягушки, служит приспособлением как к водному, так и к наземномуобразу жизни. Кратко!

Математика, 7 лет назад

Вокруг рыцарского замка возводят стены. За 1 час на каждый из 4 стен укладывают 12 камней, скреплённых раствором. Сколько камней будет уложено на 4 стенах за неделю, если работа будет идти непрерывно...