Алгебра, вопрос задал Аноним , 1 год назад

помогите срочно даю 100 баллов

Приложения:

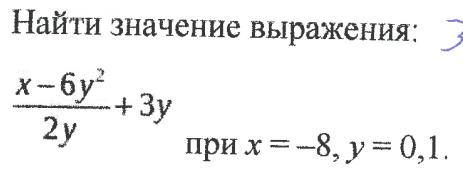
Ответы на вопрос

Ответил Universalka

1

$\displaystyle\bf\\1)\\\\\frac{x-6y^{2} }{2y} +3y$

Сначала упростим выражение , а потом найдём его значение при заданных значениях переменных :

$\displaystyle\bf\\\frac{x-6y^{2} }{2y} +3y=\frac{x-6y^{2} +2y\cdot 3y}{2y} =\frac{x-6y^{2} +6y^{2} }{2y} =\frac{x}{2y} \\\\x=-8 \ \ ; \ \ y=0,1\\\\\frac{x}{2y} =\frac{-8}{2\cdot 0,1} =-\frac{8}{0,2} =-40\\\\Otvet \ : \ -40\\\\\\2)\\\\x^{2} =49\\\\x_{1,2} =\pm \ \sqrt{49} =\pm \ 7\\\\Otvet \ : \ -7 \ ; \ 7\\\\3x^{2} =18x\\\\3x^{2} -18x=0\\\\3x\cdot(x-6)=0\\\\\\\left[\begin{array}{ccc}x=0\\x-6=0\end{array}\right\\\\\\\left[\begin{array}{ccc}x_{1} =0\\x_{2} =6\end{array}\right$

$\displaystyle\bf\\Otvet \ : \ 0 \ ; \ 6\\\\100x^{2} -16=0\\\\(10x)^{2} -4^{2} =0\\\\(10x-4)\cdot(10x+4)=0\\\\\\\left[\begin{array}{ccc}10x-4=0\\10x+4=0\end{array}\right\\\\\\\left[\begin{array}{ccc}10x=4\\10x=-4\end{array}\right\\\\\\\left[\begin{array}{ccc}x_{1} =0,4\\x_{2} =-0,4\end{array}\right\\\\\\Otvet \ : \ 0,4 \ ; \ -0,4\\\\\\3)\\\\\frac{12}{\sqrt{x} -2}$

Знаменатель дроби не должен равняться нулю , так как на ноль делить нельзя .

$\displaystyle\bf\\\sqrt{x} -2\neq 0\\\\\sqrt{x} \neq 2\\\\x\neq 4$

Выражение имеет смысл при всех действительных значениях переменной x , кроме x = 4 , то есть :

$\displaystyle\bf\\Otvet \ : \ x\in(-\infty \ , \ 4) \ \cup \ (4 \ ; \ +\infty)$

Universalka: А почему оценка 4 ?

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

8. 3 однієї гілки у протилежних напрямках одночасно почали повзти два равлики. Швидкість одного з них 13,6 см/хв, а другого на 0,9 см/хв менша. Через скільки хвилин відстань між ними буде 34.19 см?

Українська мова, 1 год назад

6. Вкажіть, у якому рядку наведено складне речення. а) Хотів пастух почути голос Бога в палаючім - 6) послала мати по гриби хлопчину, і в темнику кущi i запалив маленький вiн загубив стежки...

Математика, 1 год назад

8. Вычисли рационально. 9 4 · 10 ● 9. Определи поя поте по Э- C 3 · 29...

Английский язык, 1 год назад

Presentation Skills м...

География, 6 лет назад

Что изменили люди в гибралтаре...

Русский язык, 6 лет назад

ПОМОГИТЕ дам 50 баллов , задание вроде легкое по 10 слов прилагательных с Н-НН на следующие группы: 1)стык корня и суффикса; 2)суффиксы ОНН\ЕНН; 3)суффиксы АН\ЯН; 4)суффиксы ИН.