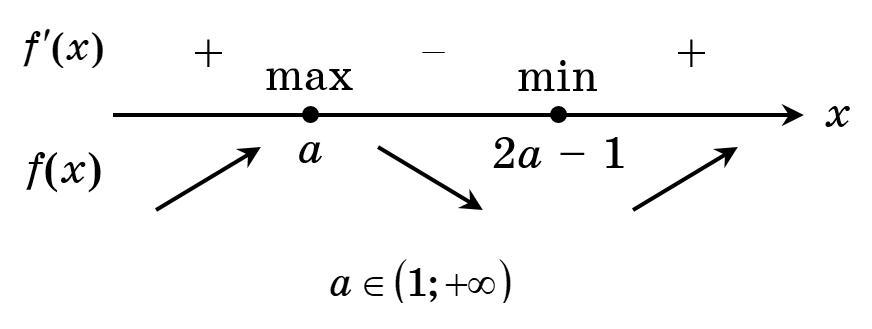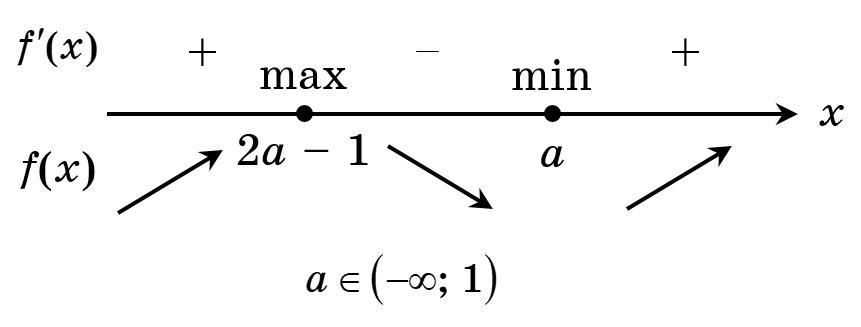Помогите с заданиями пожалуйста)))

Знайдемо похідну від функції

а) Критичною точкою функції називається точка, у якій похідна цієї функції дорівнює нулю.

Отже, розв'яжемо квадратне рівняння залежно від значень параметра

Знайдемо дискримінант цього рівняння:

Розглянемо два випадки.

1) Якщо , тобто , то маємо дві критичні точки.

, тобто

Отже, при маємо дві критичні точки:

2) Якщо , тобто то маємо одну критичну точку:

б) Точками екстремуму функції називаються критичні точки, при переході через яких похідна змінює свій знак на протилежний.

Теорема Ферма (необхідна умова екстремуму): якщо точка  є точкою екстремуму функції і в цій точці існує похідна, то вона дорівнює нулю: (див. пункт а).

Теорема (достатня умова екстремуму): якщо функція неперервна в точці та:

1) на проміжку і на проміжку , то є точкою максимуму функції ;

2) на проміжку і на проміжку , то є точкою мінімуму функції .

Якщо , то:

1) при маємо: (див. рисунок).

2) при маємо: (див. рисунок).

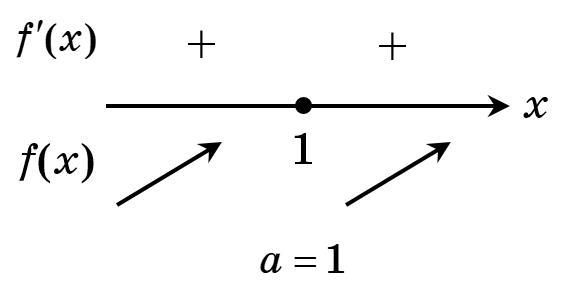
Якщо , то немає точок екстремуму (див рисунок).

в) Ознака зростання та спадання функції: якщо у кожній точці проміжку , то функція зростає на

З рисунків можна дійти висновку:

1) Якщо , то функція зростає на та спадає на .

2) Якщо , то функція спадає на та спадає на .

3) Якщо , то функція зростає на всій області визначення.

Відповідь:

а) Якщо , то маємо дві критичні точки:

Якщо , то маємо одну критичну точку:

б) Якщо , то

Якщо , то

Якщо , то немає точок екстремуму.

в) Якщо , то функція зростає на та спадає на .

Якщо , то функція спадає на та спадає на .

Якщо , то функція зростає на всій області визначення.

Знайдемо похідну від функції

Прирівняємо похідну до нулю:

Оскільки — можливо одна з точок екстремуму функції , то підставимо її в рівняння і розв'яжемо його відносно :

Отже, при та точка є точкою екстремуму функції

Відповідь: