Алгебра, вопрос задал patrickaaarina , 2 года назад

ПОМОГИТЕ С ЗАДАНИЯМИ ПО МАТЕМАТИКЕ. НЕ МОГУ РЕШИТЬ

Приложения:

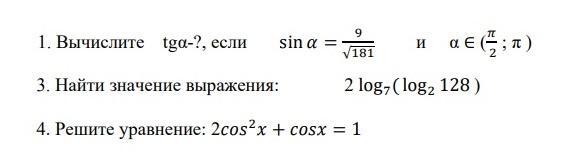
Ответы на вопрос

Ответил daraprelj

1. Воспользуемся формулой $1 + ctg a^{2} = \frac{1}{sina^{2} }$

$ctg a = \sqrt{\frac{1}{sina^{2} }-1 }$

Т.к. а∈( $\frac{\pi }{2} ; \pi$ ) => ctg a и tg a будут отрицательными

$- ctg a = - \sqrt{1 : (\frac{9}{\sqrt{181} })^{2} -1 } = - \sqrt{1 * (\frac{181}{{81} }) -1 } = - \sqrt{2 \frac{19}{81} - 1 } =$

$= - \sqrt{1\frac{19}{81} } = - \sqrt{\frac{100}{81} } = - \frac{10}{9}$

Теперь воспользуемся формулой $tg a = \frac{1}{ctg a}$

$tg a = 1 : (-\frac{10}{9}) = 1 * (-\frac{9}{10}) = -\frac{9}{10} = - 0,9$

3. $2 log_{7} (log_{2} 128) = 2 log_{7} 7 = 2*1=2$

4. $2 cos^{2}x+ cosx=1$

Пусть cos x = t, тогда

2t²+t-1=0

D = 1²-4*2*(-1)=1+8=9=3²

$t_{1} = \frac{-1+3}{2*2} = \frac{2}{4} = \frac{1}{2}$

$t_{2} = \frac{-1-3}{2*2} = - \frac{4}{4} = -1$

Вернёмся к замене

$cosx= \frac{1}{2}$

x = ± arccos 0,5 + 2πn , n∈Z

x = ± π/3 + 2πn , n∈Z

cos x = -1

x = π + 2πk , k∈Z

Новые вопросы

Қазақ тiлi, 1 год назад

Другие предметы, 1 год назад

Физика, 2 года назад

Английский язык, 2 года назад

Алгебра, 7 лет назад

Математика, 7 лет назад