Алгебра, вопрос задал dkeow9so , 6 лет назад

Помогите с заданием прошу

Приложения:

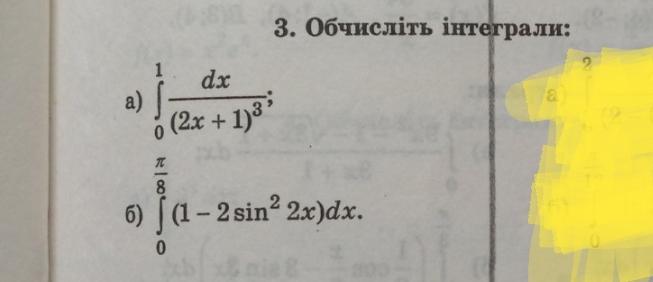
Ответы на вопрос

Ответил Viis5

0

a) $I = \int\limits_0^1 \frac{dx}{(2x+1)^3}$

$2x+1 = t$

$d(2x+1) = dt$

$2dx = dt$

$dx = \frac{dt}{2}$

$x = 0\; t=1$

$x=1\; t = 3$

$I = \int\limits_1^3 \frac{\frac{dt}{2}}{t^3} = \frac{1}{2}\cdot\int_1^3 t^{-3} dt =$

$= \frac{1}{2}\cdot\frac{t^{-3+1}}{-3+1}|_1^3 = \frac{1}{2}\cdot\frac{1}{-2}\cdot t^{-2}|_1^3 =$

$= -\frac{1}{4}\cdot (3^{-2} - 1^{-2}) = -\frac{1}{4}\cdot (\frac{1}{9} - 1) =$

$= \frac{1}{4}\cdot (1 - \frac{1}{9}) = \frac{1}{4}\cdot\frac{8}{9} = \frac{2}{9}$

б) $I = \int\limits_0^{\frac{\pi}{8}} (1 - 2\sin^2(2x)) dx =$

$= \int\limits_0^{\frac{\pi}{8}} \cos(4x) dx$

$4x = t$

$d(4x) = dt$

$4dx = dt$

$dx = \frac{dt}{4}$

$x = 0\: t = 0$

$x = \frac{\pi}{8}\: t = \frac{\pi}{2}$

$I = \int\limits_0^{\frac{\pi}{2}} \cos(t) \frac{dt}{4} =$

$= \frac{1}{4}\cdot \sin(t)|_0^{\frac{\pi}{2}} =$

$= \frac{1}{4}\cdot (\sin(\frac{\pi}{2}) - \sin(0)) = \frac{1}{4}\cdot (1 - 0) = \frac{1}{4}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

сочинение на тему Астана на казахском языке 7-8 предложений...

Английский язык, 1 год назад

Сделайте пожалуйста номер 4, он относится к тексту.

Математика, 6 лет назад

-1/6 - 2, нужно дробью...

Физика, 6 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!!!!!! ДАЮ 25 БАЛЛОВ сколько теплоты выделяется при отвердевании железа массой 500г при температуре 1535 градусов(нужно полностью решение)...

Математика, 8 лет назад

Запишите несколько формул линейных функций, графики которых параллельны графику функции : 1) у= -1,5 2) у=7/11 3) у=0...

История, 8 лет назад

у якому зхначеннi сьогоднi вживають слово iнiцiал?