Помогите с задачей.
В треугольнике ABC дано: AB=3, AC=5 и BC=6. Найти расстояние от вершины C до высоты, опущенной из вершины B на сторону AC.
Ответы на вопрос
Ответил 8286505
0
p=(a+b+c):2=(3+5+6):2=14:2=7 см
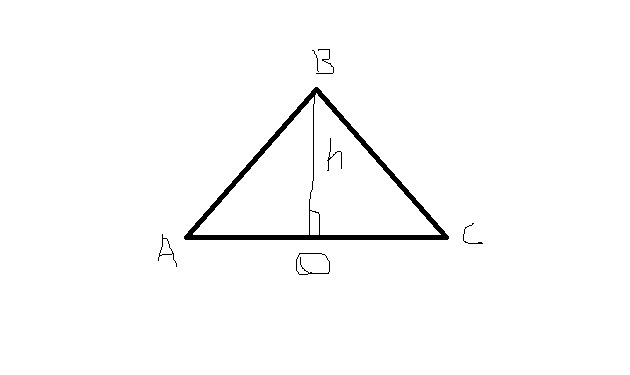
поскольку высота ВО (расстояние измеряется по перпендикуляру, по условию) образует прямоугольный треугольник, в котором сторона ОС является катетом, то найдем его по формуле
AO>AC, следовательно ∠ВАС является тупым и высота опущена на продолжение АС
Приложения:
Ответил Kirk2608
0
мне кажется, что это неполное решение.
Ответил Kirk2608
0
Вы нашли только высоту в треугольнике ABC, а надо расстояние от вершины С до данной высоты. Я правильно понимаю же условие задачи?
Ответил 8286505
0
а, точно сча доделаю спс
Ответил 8286505
0
спс, исправила
Ответил Kirk2608
0
и почему то мне опять кажется, что не то.
Новые вопросы