Помогите с решением пожалуйста
Приложения:
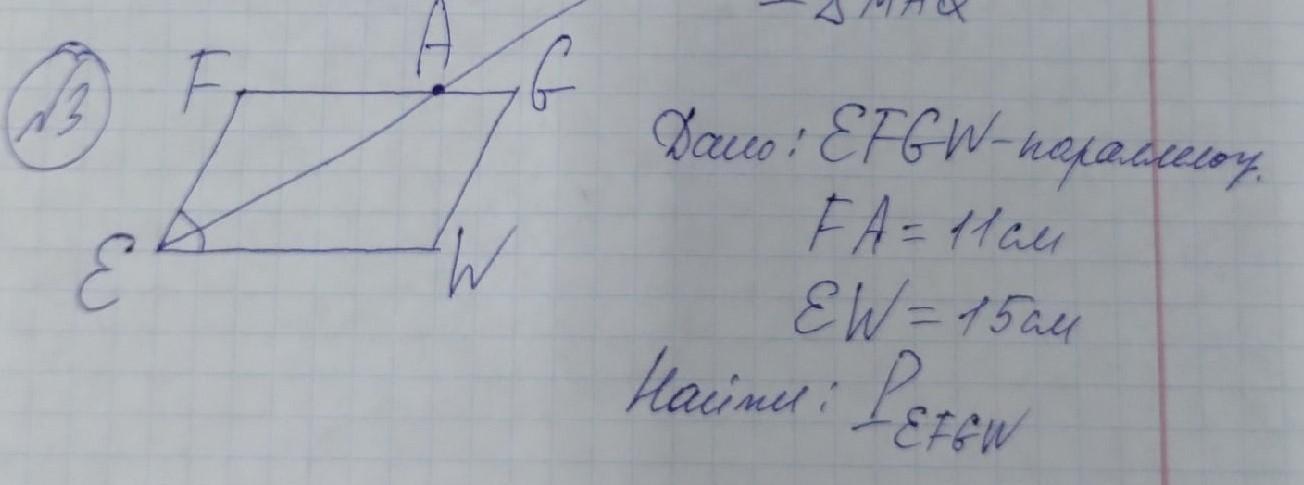
Ответы на вопрос
Ответил ReMiDa
1
Ответ:
Периметр параллелограмма равен 52 см
Объяснение:
Дан параллелограмм EFGW, EA - биссектриса ∠E. FA=11см, EW=15 см.Требуется найти периметр EFGW.
- Параллелограмм - это четырёхугольник, у которого противоположные стороны попарно параллельны и равны.
- Периметр параллелограмма равен удвоенной сумме прилежащих сторон:
Так как сторона EW нам известна, решение задачи сводится к нахождению стороны EF.
EA - биссектриса угла Е.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Это легко доказать.
∠FEA=∠WEA - по определению биссектрисы.
∠WEA=∠FAE - как внутренние накрест лежащие углы при параллельных прямых FG и EW и секущей EA. ⇒∠FEA=∠FAE. А если углы при основании равны, то треугольник равнобедренный.
В равнобедренном треугольнике боковые стороны равны: EF=FA=11 см
Теперь находим периметр параллелограмма:
см
Новые вопросы