Математика, вопрос задал margorita975 , 7 лет назад

!!!!!!!!!!!!!!Помогите с решением лимитов( с объяснением)7,9,10,12 ПРИМЕРЫ

Приложения:

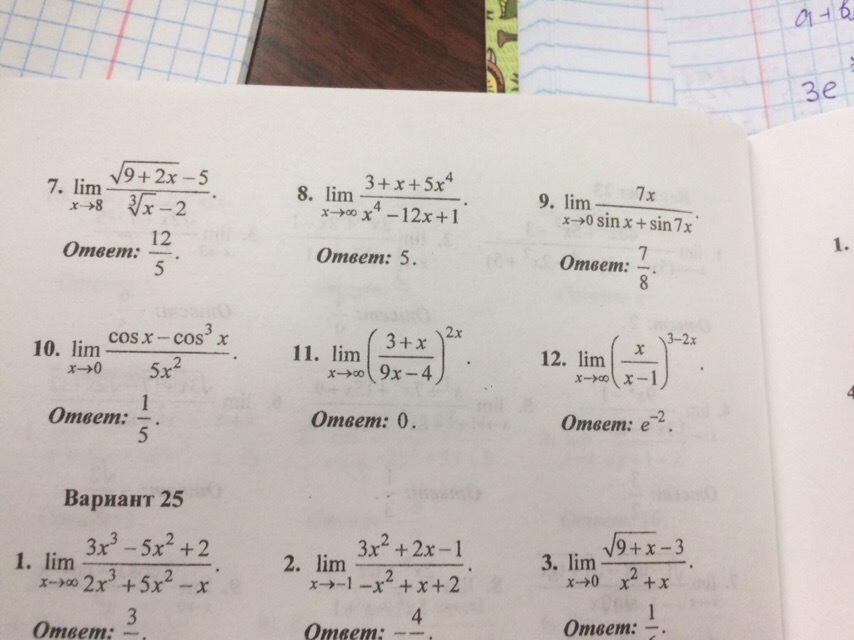
Ответы на вопрос

Ответил NNNLLL54

$7); ; limlimits _{x to 8}frac{sqrt{9+2x}-5}{sqrt[3]{x}-2}=limlimits _{x to 8}frac{(9+2x-25)(sqrt[3]{x^2}+2sqrt[3]{x}+4)}{(x-8)(sqrt{9+2x}+5)}=\\=limlimits _{x to 8}frac{2(x-8)(sqrt[3]{x^2}+2sqrt[3]{x}+4)}{(x-8)(sqrt{9+2x}+5)}=frac{2(sqrt[3]{8^2}+2sqrt[3]{8}+4)}{sqrt{25}+5}=frac{2(4+4+4)}{10}=frac{12}{5}$

$9); ; limlimits _{x to 0}frac{7x}{sinx+sin7x}=limlimits _{x to 0}frac{7x}{2sin4xcdot cos3x}=Big [, sinalpha sim alpha ; ,; alpha to 0; Big ]=\\=limlimits _{x to 0}frac{7x}{2cdot 4xcdot cos3x}=frac{7}{2cdot 4cdot 1}=frac{7}{8}\\10); ; limlimits _{x to 0}frac{cosx-cos^3x}{5x^2}=limlimits _{ xto 0}frac{cosxcdot (1-cos^2x}{5x^2}=limlimits _{x to 0}frac{-cosxcdot sin^2x}{5x^2}=\\=limlimits _{x to 0}frac{cosxcdot x^2}{5x^2}=limlimits _{x to 0}frac{cosx}{5}=frac{1}{5}$

$12); ; limlimits _{x to infty }Big (frac{x}{x-1}Big )^{3-2x}=limlimits _{x to infty }Big (1+frac{1}{x-1}Big )^{frac{x-1}{1}cdot frac{3-2x}{x-1}}=\\=limlimits _{x to infty }Big (Big (1+frac{1}{x-1}Big )^{x-1}Big )^{frac{3-2x}{x-1}}=e^{limlimits _{x to infty}frac{3-2x}{x-1}}=e^{-2}=frac{1}{e^2}$

Ответил margorita975

Спасибо большое!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

по англійськи скласти діалог по темі унувермаг...

Русский язык, 1 год назад

гвоздик -звукобуквенный разбор слова...

Алгебра, 7 лет назад

Исследуйте функцию на монотонность. Пожалуйста с решением.

Биология, 7 лет назад

Девятое задание 30 баллов...

Математика, 8 лет назад

а) 5,7*13 б)Упростите и найдите значение выражения 1,2а+1/3+5,6а, если а= 5/51 ------------- 7,41*10...

Литература, 8 лет назад

В А Жуковский Кубок кто из героев балады не понравился и почему?