Математика, вопрос задал kardibalet , 11 месяцев назад

помогите с решением этих заданий

Приложения:

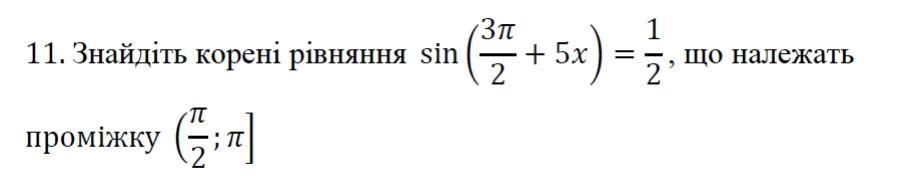
kardibalet: ПОЖАЛУЙСТА

Ответы на вопрос

Ответил NNNLLL54

Ответ:

Тригонометрическое уравнение .

$\displaystyle \bf sin\Big(\frac{3\pi }{2}+5x\Big)=\frac{1}{2}\ \ ,\ \ \ \ x\in \Big(\frac{\pi }{2}\ ;\ \pi \ \Big]$

По формулам приведения имеем : $\bf sin\Big(\dfrac{3\pi }{2}+5x\Big)=-cos\, 5x$ .

Поэтому уравнение перепишем в виде :

$\displaystyle \bf cos\, 5x=-\frac{1}{2}\\\\5x=\pm arccos\Big(-\frac{1}{2}\Big)+2\pi n\ \ ,\ \ n\in Z\\\\5x=\pm \Big(\pi -arccos\frac{1}{2}\Big)+2\pi n\\\\5x=\pm \Big(\bf \pi -\frac{\pi }{3}\Big)+2\pi n\ \ ,\ \ n\in Z\\\\5x=\pm \frac{2\pi }{3}+2\pi n\ \ ,\ \ n\in Z\\\\x=\pm \frac{2\pi }{15}+\frac{2\pi n}{5}\ \ ,\ \ n\in Z$

Найдём корни уравнения, принадлежащие указанному промежутку .

$\displaystyle \bf x\in \Big(\frac{\pi }{2}\ ;\ \pi \ \Big]\ :\ \ x_1=\frac{2\pi }{15} +\frac{2\pi}{5} =\frac{8\pi }{15}\ ,\ \ x_2=\frac{2\pi }{15} +\frac{4\pi}{5} =\frac{14\pi }{15}\ \ ,\\\\\\x_3=-\dfrac{2\pi }{15}+\dfrac{4\pi }{5}=\dfrac{10\pi }{15}=\frac{2\pi }{3}\ .$

Приложения:

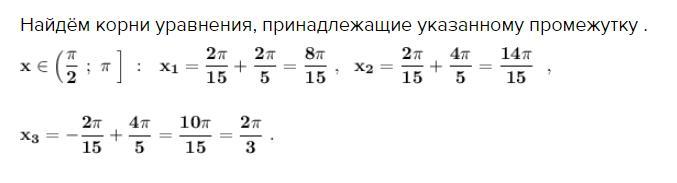
kardibalet: есть еще задания в профиле по математике именно, там их два еще вроде

kardibalet: если есть желание решить

Предыдущий вопрос

Следующий вопрос

Новые вопросы

История, 11 месяцев назад

4. У якій країні діяли «закони Хаммурапі»? Назвіть головний принцип законів Хаммурапі. даю 10 балов...

Биология, 11 месяцев назад

У рядку викресліть зайвий термін. Поясніть свій вибір кіт лісовий, страус, морська зірка, слимак виноградний...

Биология, 11 месяцев назад

Укажіть характеристики плевральної порожнини: А) заповнена повітрям Б) має від'ємний тиск В) заповнена жировою тканиною Г) має підвищений тиск...