Алгебра, вопрос задал Elegantnaya , 1 год назад

Помогите с производной. Задание номер 1, 1 пример СРОЧНО!!! Найти производную

Приложения:

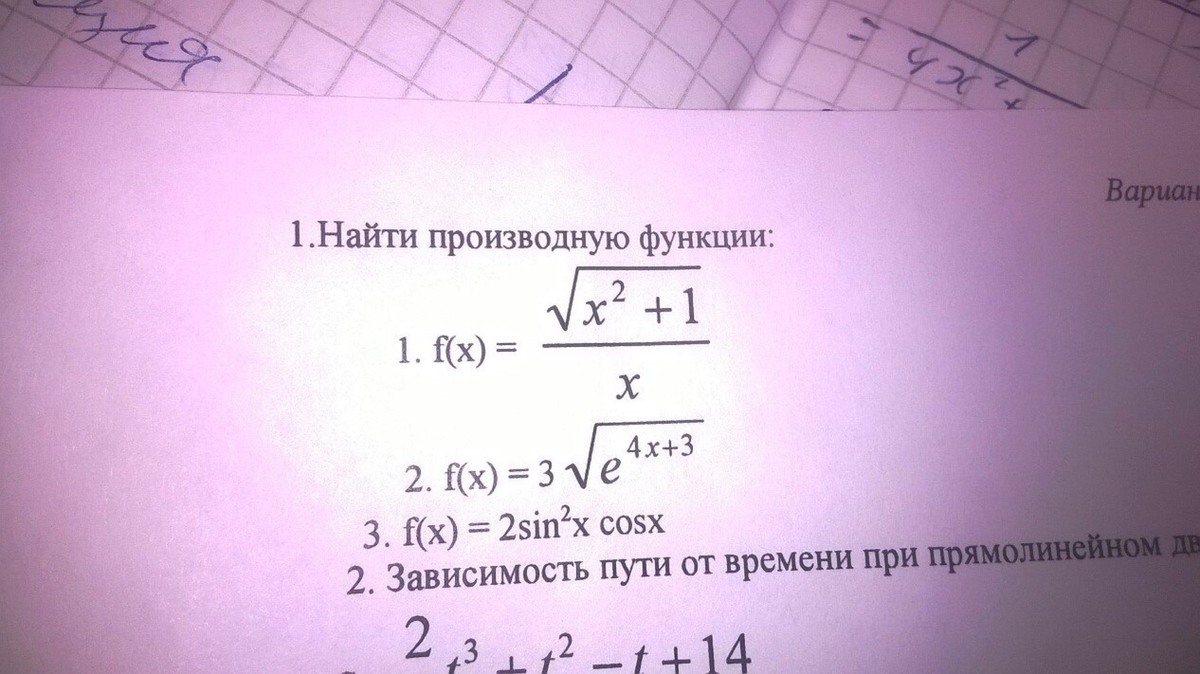
yellok: решить только 1,1 да?

Elegantnaya: да!:)

Ответы на вопрос

Ответил yellok

$f(x)= \frac{ \sqrt{ x^{2} +1} }{x}$
$f'(x)= (\frac{ \sqrt{ x^{2} +1} }{x} )'= \frac{( \sqrt{ x^{2} +1})'*x-(x)'* \sqrt{ x^{2} +1} }{ x^{2} } = \frac{ \frac{( x^{2} +1)'}{2 \sqrt{ x^{2} +1} }*x-1* \sqrt{ x^{2} +1} }{ x^{2} }$ $=\frac{ \frac{2x}{2 \sqrt{ x^{2} +1} }*x- \sqrt{ x^{2} +1} }{ x^{2} } =\frac{ \frac{ x^{2} }{ \sqrt{ x^{2} +1} }- \sqrt{ x^{2} +1} }{ x^{2} }= \frac{ x^{2} - ( \sqrt{ x^{2} +1} )^{2} }{ x^{2} \sqrt{ x^{2} +1} }= \frac{ x^{2} - x^{2} -1}{x^{2} \sqrt{ x^{2} +1}}$ $= \frac{-1}{x^{2} \sqrt{ x^{2} +1}}$

Elegantnaya: Спасибо, Вам огромное!:))

yellok: не за что)))

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

Существует ли 1000-значное число n, запись которого не содержит цифры 0, равное сумме двух слагаемых, каждое из которых получается перестановкой цифр числа n.

Математика, 1 год назад

Пожалуйста решите примеры!! Если можно по действиям 199*(354-290)+1600= 291:(165+15+90)-160= 1500-910+(693:3*2)+45= Не просто одни ответы!!! Что бы по действиям, заранее спасибо...

Математика, 1 год назад

составить уравнение касательной проведенной к графику функции y=3x-x^3 в точке с абсциссой x0=0...

Экономика, 1 год назад

К источникам кредитных ресурсов можно отнести: а) доходы гос-ва от предпринимательской деятельности, которые сразу направляются на выплаты пенсий и пособий; б) часть прибыли предприятия, которая...

Математика, 7 лет назад

корень из 2/2 + cos 2x =0...

Алгебра, 7 лет назад

f(x)=-1/3x^3+x^2+3x f'(x)>0...