Математика, вопрос задал Taylor1799 , 2 года назад

Помогите с пределами​

Приложения:
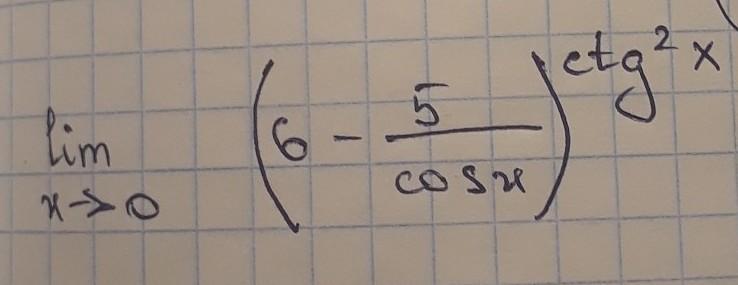
olgaua64: Вместо х поставь 0
Guerrino: с каких пор там есть значение?

Ответы на вопрос

Ответил Guerrino
0

Разложим показатель и основание по формуле Тейлора до o(x^2):

\cot ^2 x = \frac{1}{x^2}-\frac{2}{3}+\frac{x^2}{15}+o(x^2),\; x\to 0, 6-\frac{5}{\cos x} = 1-\frac{5x^2}{2}+o(x^2),\; x\to 0.

Искомый предел: \lim\limits_{x\to 0}\left(1-\frac{5x^2}{2}+o(x^2)\right)^{\frac{1}{x^2}-\frac{2}{3}+\frac{x^2}{15}+o(x^2)}=\lim\limits_{x\to 0}\left(1-\frac{5x^2}{2}\right)^{\frac{1}{x^2}}= e^{-5/2}.

Taylor1799: спасибо, а возможно решение через замечательный предел?
Czaryok: Здравствуйте, можете помочь с заданием? https://znanija.com/task/41738593
Guerrino: ну в конце и используется замечательный предел
Taylor1799: просто решение через Тейлора мы не изучали) даже не понимаю, что происходит
Guerrino: подумайте как заменой (и некоторым преобразованием) свести этот предел к пределу lim{u -> 0} (1+5u/(u+1))^(-0,5/u), затем можно заменить u/(u+1) = t, откуда вообще все будет очевидно. общее соображение состоит в том, чтобы привести именно основание степени к хорошему виду
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Английский язык, 1 год назад
Add -(e)d to the verbs and put them in the correct column, then read them out. Cry, stay, stop, hate ,taste, prefer, fry, dance, like, type, plan, annoy, destroy, pray, phone, beg , try, tip, play,...
Русский язык, 1 год назад
Во что превратила злая ведьма уточку в сказке "Белая уточка"?
История, 2 года назад
РЕБЯТ ПОМОГИТЕ ПЖ! СОР ПО ИСТОРИИ КАЗАХСТАНА ТОЛЬКО ОДНО ЗАДАНИЕ НЕ СМОГ СДЕЛАТЬ Проанализируйте по формуле тему «Ассамблея народа Казахстана – фундамент мира и пример межнационального согласия»...
Другие предметы, 2 года назад
Для чего создан виртуальное пространство?​
История, 7 лет назад
Почему за кражу вещи, скотины и раба наказывали одинаково ?
Обществознание, 7 лет назад
что такое чувственное познание...