помогите с параметром пж
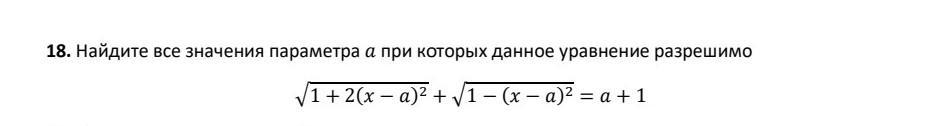
Ответы на вопрос
Ответ: a∈[√3-1 ; (3*√2 -2)/2]
Объяснение:
Замена:
√(1+2*(x-a)^2)=m>=1 ( 2*(x-a)^2=m^2-1>=0 →m>=1)
√(1-(x-a)^2)=n>=0 ( -(x-a)^2=n^2-1<=0 ; n^2<=1 → n∈[0;1] )
a+1=t>1 (пока оставим в такой оценке,тк мы не знаем точное минимальное значение выражения m+n)
Тогда уравнение эквивалентно системе:
m^2+2n^2=3 (заметим что если n∈[0;1] ,то m>=1)
m+n=t → m=t-n
(t-n)^2+2n^2=3
t^2-2*n*t+n^2 +2n^2-3=0
f(n)=3n^2-2*n*t +(t^2-3)=0
Таким образом приходим к обычной задаче.
Нужно найти такие значения параметра t, когда существует хотя бы один корень с промежутка n∈[0;1] , в этом случае √(1-(x-a)^2)=n разрешено относительно n, а значит имеет решение .
1. Рассмотрим случай , когда 1 корень лежит на интервале n∈[0;1] ,а другой нет. Очевидно ,что это произойдет когда 0 лежит внутри параболы, а 1 вне параболы, либо когда 1 лежит внутри параболы, а 0 лежит вне параболы. Либо когда парабола пересекает 1 или 0.
Таким образом ,тк A=3 >0 (ветви идут вверх):
1) f(0)>=0 ; f(1)<=0 (заметим , что выполнение данного условия гарантирует существование корней)
2) f(1)>=0 ; f(0) <=0 (так же гарантирует существование корней)
Это равносильно неравенству:
f(1)*f(0)<=0
f(0)=t^2-3=(t-√3)*(t+√3)
f(1)=3-2t+t^2-3=t^2-2t=t*(t-2)
Получаем неравенство:
t*(t-2)*(t-√3)*(t+√3)<=0
Решаем методом интервалов:
+ (-√3) - 0 + √3 - 2 +
тк нам нужно решение t>1 ,то
t∈[√3;2]
2. Рассмотрим случай когда оба корня лежат на интервале n∈[0;1].
В этом случае не один из корней не лежит внутри параболы,но чтобы исключить возможность того, что не один из корней не лежит на интервале n∈[0;1] нужно дополнительное условие ,что вершина параболы лежит на промежутке n∈[0;1]. Так же необходимо существование решений D>=0 ,тк первые два условия еще не гарантируют существование решений:
f(1)>=0
f(0)>=0
0<nв<1
D>=0
Так же не забываем ,что t>1
t*(t-2)>=0 → t∈[2;∞) (c учетом t>1)
(t-√3)*(t+√3)
>=0 →t∈[√3;∞]
nв=2t/6=t/3
0<t/3<1 → 0<t<3 → 1<t<3
D/4=t^2-3*(t^2-3)= -2t^2+9>=0
2t^2<=9 → 1<t<3/√2.
Пересекая все решения имеем:
t∈[2;3/√2]
Таким образом:
t∈[√3; 3*√2/2]
Или: (a=t-1)
a∈[√3-1 ; (3*√2 -2)/2].
Теперь решим вторым способом,применяя экстремум.
Предварительно сделав замену (x-a)=t
Запишем функцию:
f(t)=√(1+2t^2) +√(1-t^2)
Область определения: |t|<=1 (функция ограничена , а значит имеет минимум и максимум на отрезке t∈[-1;1] ,так же на этом отрезке она является непрерывной)
Найдем производную и приравняем к нулю:
f'(t)= 4t/2*√(1+2t^2) - 2t/2*√(1-t^2)=0
t* (2/√(1+2t^2) -1/√(1-t^2) )=0 ( t≠+-1)
t*(2*√(1-t^2) -√(1+2t^2) )=0
t1=0
2*√(1-t^2)=√(1+2t^2)
4*(1-t^2)=1+2t^2
6t^2-3=0
t^2=1/2
t=+-1/√2
Осталось найти значения функций в точках :
t=0 ;+-1/√2 ;+-1 (на краях интервала тоже нужно проверять)
f(0)=√1 +√1=2
f(+-1)=√(1+2) +√(1-1)=√3
f(+-1/√2)=√(1+2*1/2) +√(1-1/2)=√2+√(1/2)= √2 +1/√2 =3/√2=3*√2/2
fmin=√3
fmax=3*√2/2
Таким образом,тк функция непрерывна на интервале t∈[-1;1] : a+1=[√3; 3*√2/2]
a∈[√3-1 ; (3*√2 -2)/2].
Как видим ,это более простой путь, хоть и требует знания экстремума функции.