Помогите с олимпиадой:
1) Над девятизначным числом разрешается производить следующее действие: любую цифру числа можно заменить на последнюю цифру суммы цифр этого числа. Можно ли с помощью таких действий из числа 133355555 получить число 123456789?
2) Внутри квадрата ABCD отмечены точки К и М (точка М находит- ся внутри треугольника ABD, точка К - внутри ВМС") так, что треугольники ВАМ и DKM равны (AM = KM, BM = MD, AB = KD), Найдите Угол KCM, если Угол AMB = 100°
3) (картинка 1): Квадрат 6 х 6 разрезали на четырехклеточные и пятиклеточные фигуры, равные показанными на рисунке (обе фигуры участвовали в разрезе). Сколько таких фигур было использовано?
4) Даны квадратные трехчлены x^{2} + ax + b, x^{2} + bx + d, x^{2} + ex + f
Оказалось, что любые 2 из них имеют общий корень, но все три общего корня не имеют. Докажите, что выполнены ровно два неравенства из следующих трех:
\frac{a^{2}+c^{2}-e^{2}}{4} > b + d - f
\frac{e^{2}+c^{2}-a^{2}}{4} > d + f - b
\frac{e^{2}+a^{2}-c^{2}}{4} > f + b - d
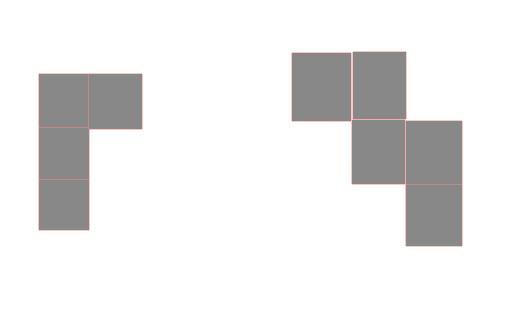
Ответы на вопрос
1) Сумма цифр 35, последняя пятерка, нечетное. Все цифры в 133355555 тоже нечетные. Если заменим любую нечетную цифру на нечетную, то сумма цифр нового числа снова будет нечетной, и т.д. То есть мы никогда не получим последнюю цифру суммы четной, и получить число, содержащее четные цифры не возможно.
2) Поскольку ВМ=МD, значит М лежит на диагонали АС. В треугольнике АМВ угол ∠АМВ=100°, а ∠ВАМ=45°, значит ∠АВМ=180°-100°-45°=35°
Треугольник ВАМ равен DKM, также BAM равен DAM/
Значит ∠КDC = ∠ADC-∠ADM-∠MDK = 90-35-35=20°
Но СD=AB=KD, значит треугольник КDС равнобедренный, и угол КСD равен (180-20)/2 = 80°
А искомый угол KCM равен ∠KCD- ∠ACD = 80°-45°=35°
Ответ: ∠KCM=35°
3) Квадрат можно разрезать на 4+4 фигуры 4*4+4*5=36, по другому 36 не получится.
Фигуры 1,4,5,8 - Г-образные, 2,3,6,7 - w-образные
1 1 2 2 3 4
1 2 2 3 3 4
1 2 3 3 4 4
5 5 6 6 7 8
5 6 6 7 7 8
5 6 7 7 8 8