Помогите с интегралами..
Приложения:
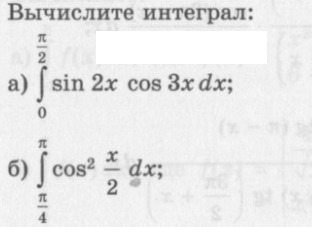
Ответы на вопрос
Ответил Аноним
0
∫(2sinx*cosx(4cos^3x-3cosx)dx=∫(8cos^4x*sinx-6cos^2x*sinx)dx=
=8∫cos^4x*sinx*dx-6∫cos^2x*sinx*dx=
(t=cosx; dt=-sinxdx)
=-8∫t^4dt+6∫t^2dt=-8*t^5/5+6*t^3/3=2t^3-1.6*t^5=
=2*cos^3x-1.6*cos^5x=0-0-2*1+1.6=-0.4
2)∫(1+cosx)/2dx=∫0.5dx+0.5∫cosxDx=0.5x+0.5*sinx=
=0.5pi+0.5*0-pi/8-√2/4=3pi/8-√2/4
=8∫cos^4x*sinx*dx-6∫cos^2x*sinx*dx=
(t=cosx; dt=-sinxdx)
=-8∫t^4dt+6∫t^2dt=-8*t^5/5+6*t^3/3=2t^3-1.6*t^5=
=2*cos^3x-1.6*cos^5x=0-0-2*1+1.6=-0.4
2)∫(1+cosx)/2dx=∫0.5dx+0.5∫cosxDx=0.5x+0.5*sinx=
=0.5pi+0.5*0-pi/8-√2/4=3pi/8-√2/4
Ответил Аноним
0
1) я разложила синус двойного угла как удвоенное произведение синуса на косинус
Ответил Аноним
0
и cos3x=4cos^3x-3cosx
Ответил NNNLLL54
0
Сразу применить формулу sina*cosb=1/2*( sin(a+b)+sin(a-b) ) .
Ответил Аноним
0
решайте, ответ .ю я думаю, будет тот же...
Ответил NNNLLL54
0
я уже решила https://znanija.com/task/27947318
Новые вопросы