Помогите с 1-ым заданием, пожалуйста!
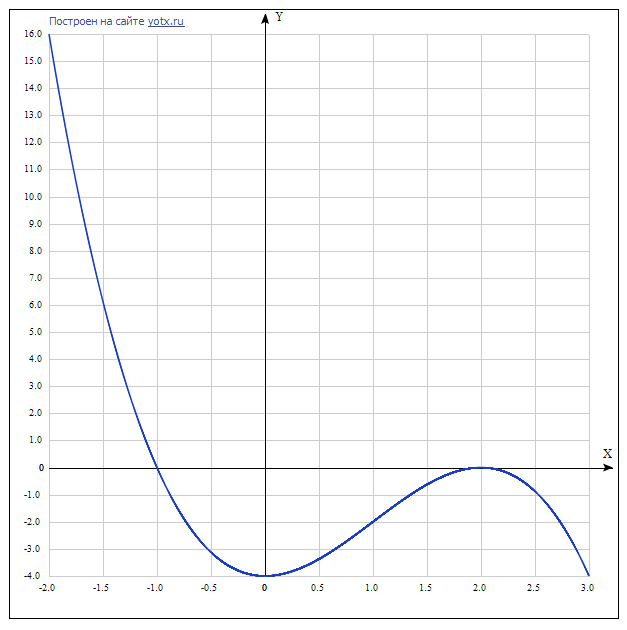
Исследуйте функцию f(x)= -x³+3x²-4 и постройте ее график
Приложения:

Ответы на вопрос
Ответил m11m
3
f(x)=-x³+3x²-4
1. Область определения функции:
D(f)=(-∞; +∞)
2. Исследуем функцию на четность:
f(-x)=-(-x)³+3*(-x)²-4=x³+3x²-4
Функция не является четной и не является нечетной.
3. Критические и стационарные точки:
f(x)' =-3x²+6x=-3x(x-2)
Производная существует всюду, значит, критических точек нет.
Стационарные точки:
f(x)' =0
-3x(x-2)=0
x=0 x=2
4. Промежутки возрастания и убывания и точки экстремума:
- + -
-------- 0 -------------- 2 --------------
При х∈(-∞; 0] функция убывает
При х∈[0; 2] функция возрастает
При х∈[2; +∞) функция убывает
х=0 - точка перегиба
f(0)=-3*0³+3*0²-4=-4
х=2 - точка перегиба
f(2) =-2³+3*2²-4=0
5. Точки для построения графика:
х| -2 | -1 | 0 | 1 | 2 | 3
y| 16| 0 | -4| -2| 0 | -4
1. Область определения функции:
D(f)=(-∞; +∞)
2. Исследуем функцию на четность:
f(-x)=-(-x)³+3*(-x)²-4=x³+3x²-4
Функция не является четной и не является нечетной.
3. Критические и стационарные точки:
f(x)' =-3x²+6x=-3x(x-2)
Производная существует всюду, значит, критических точек нет.
Стационарные точки:
f(x)' =0
-3x(x-2)=0
x=0 x=2
4. Промежутки возрастания и убывания и точки экстремума:
- + -
-------- 0 -------------- 2 --------------
При х∈(-∞; 0] функция убывает
При х∈[0; 2] функция возрастает
При х∈[2; +∞) функция убывает
х=0 - точка перегиба
f(0)=-3*0³+3*0²-4=-4
х=2 - точка перегиба
f(2) =-2³+3*2²-4=0
5. Точки для построения графика:
х| -2 | -1 | 0 | 1 | 2 | 3
y| 16| 0 | -4| -2| 0 | -4
Приложения:
LINC0LN:
Божечки, Вы - лучшая!
Новые вопросы