помогите режить пожалуйста
Приложения:
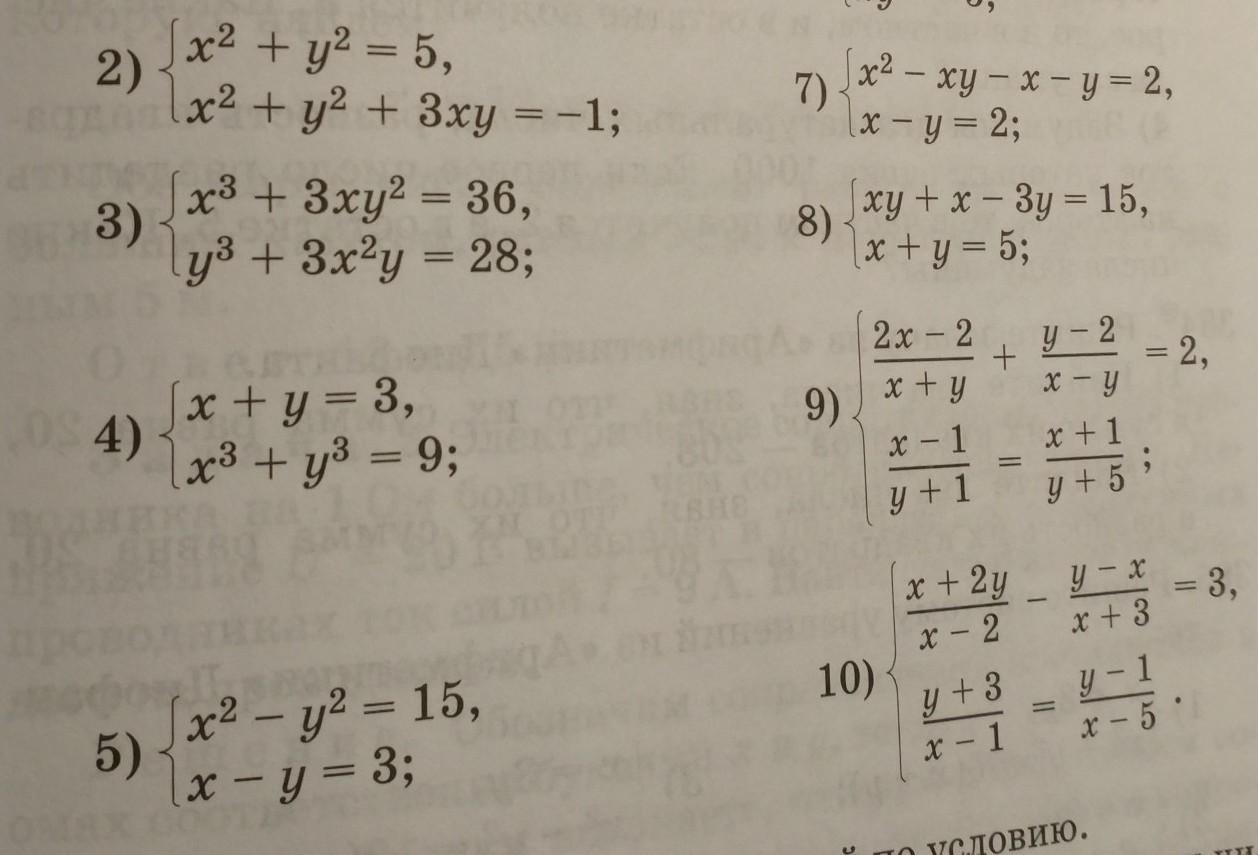
NNNLLL54:
можно выкладывать 3 примера... какие 3 решить ?
2,3,4
хотя бы
желательно все кроме 1и 5
Ответы на вопрос
Ответил NNNLLL54
1
Ответил Аноним
0
Ответ: во вложении Объяснение:
Приложения:



Новые вопросы
Математика,
1 год назад
Математика,
1 год назад
Математика,
1 год назад
Физика,
1 год назад
Математика,
6 лет назад