Алгебра, вопрос задал Sergejgho , 2 года назад

Помогите решить задания срочно, буду очень благодарен вам

Приложения:

Ответы на вопрос

Ответил natalyabryukhova

Ответ:

5. Ответ: 8

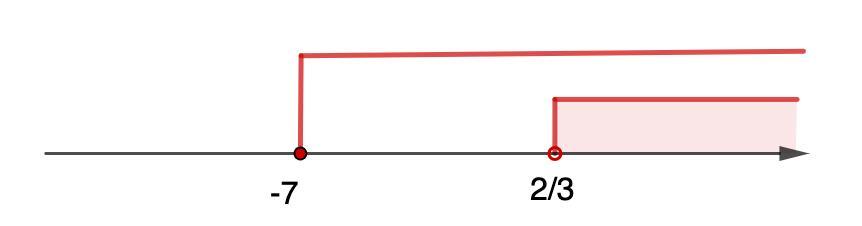
6. Ответ: (2/3; +∞)

7. Ответ: На отрезке [-6;4] функция имеет три точки экстремума.

Объяснение:

5. Решить уравнение:

$\displaystyle log_2(8+7x)=log_2(8+3x)+1$

ОДЗ:

Выражение, стоящее под знаком логарифма, должно быть положительно.

$\displaystyle \left \{ {{8+7x > 0} \atop {8+3x > 0}} \right. \;\;\;\;\;\left \{ {{x > -\frac{8}{7} } \atop {x > -\frac{8}{3} }} \right. \;\;\;\Rightarrow \;\;\;x > -\frac{8}{7}$

Перепишем уравнение в следующем виде:

$\displaystyle log_2(8+7x)=log_2(8+3x)+log_22$

Сумма логарифмов равна логарифму произведения.

$\displaystyle log_2(8+7x)=log_2(2\cdot(8+3x))\\\\ log_2(8+7x)=log_2(16+6x)$

Потенцируя, получим:

$8+7x=16+6x\\\\x=8$

х = 8 удовлетворяет условию $\displaystyle x > -\frac{8}{7}$ .

Ответ: 8

6. Решить неравенство:

$log_7(3x-2)\leq log_7(4x+5)$

ОДЗ:

$\displaystyle \left \{ {{3x-2 > 0 \atop {4x+5 > 0}} \right. \;\;\;\;\;\left \{ {{x > \frac{2}{3} } \atop {x > -\frac{5}{4} }} \right. \;\;\;\Rightarrow \;\;\;x > \frac{2}{3}$

Основания логарифмов равны, причем 7 > 1 ⇒ функция возрастающая.

Значит для выражений под знаком логарифма знак неравенства не изменится.

$3x-2\leq 4x+5\\\\-x\leq 7\;\;\;|:(-1)$

Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.

⇒ х ≥ -7

Объединим с ОДЗ:

См. рис.

Ответ: (2/3 ; +∞)

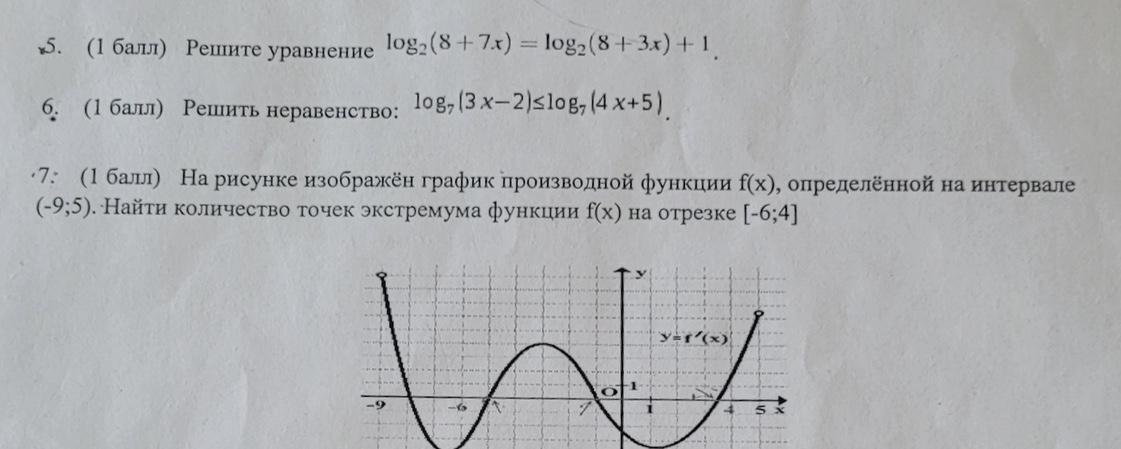
7. На рисунке изображён график производной функции f(x), определённой на интервале (-9;5). Найти количество точек экстремума функции f(x) на отрезке [-6;4].