Алгебра, вопрос задал vlados333555333555 , 2 года назад

Помогите решить задачу ребят срочно нужно ХЕЛП

Приложения:

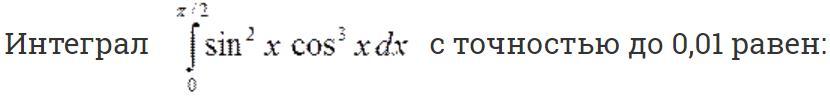
Ответы на вопрос

Ответил sangers1959

Ответ:

Объяснение:

$\int\limits^{\pi/2} _0 {sin^{2}x*cos^{3}x } \, dx =\int\limits^{\pi/2} _0 {sin^{2}x*cos^{2}x *cosx} \, dx= \int\limits^{\pi/2} _0 {sin^{2}x*(1-sin^{2}x)* cosx } \, dx =\\ =\int\limits^{\pi/2} _0(sin^{2}x-sin^{4} x)cosxdx.\\ u=sinx;du=cosxdx\\\int\limits^{\pi/2} _0(u^{2} -u^{4} )du=(\frac{u^{3} }{3} -\frac{u^5} {5} )|_{0} ^{\pi/2 } =(\frac{sin^{3}x }{3} -\frac{sin^{5}x }{5})| _{0} ^{\pi/2 }=\\$ $=\frac{sin^{3} (\pi/2) }{3} -\frac{sin^{5}(\pi/2) }{5}=\frac{1}{3} -\frac{1}{5} = \frac{5-3}{15}=\frac{2}{15}=0,13.$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

определите количество морфем в словах 1 Безмолвие 2 мог 3 растолкал 4 друг 5 протёр...

Геометрия, 1 год назад

пожалуйста, срочно :(...

Математика, 2 года назад

у школі навчаються 80 п'ятикласників. 35 відсотків усіх п'ятикласників брали участь у шкільній олімпіаді з математики. скільки п'ятикласників брало участь у шкільній олімпіаді?

Математика, 2 года назад

Відстань між містами А і В на місцевості дорівнює 360км., а на карті 6,6см,яка відстань між містами С i D на цій карті, якщо відстань між ними на місцевості дорівнює 600км.

Математика, 7 лет назад

Решите задачи: 1) В книге напечатаны рассказ и повесть, которые вместе занимают 70 стр.Повесть занимает в 4 раза больше стр., чем рассказ.Сколько страниц занимает рассказ и сколько повесть? 2)на...

Математика, 7 лет назад

в театральной кассе было 480 билетов кассир продал билеты на 5 спектаклей по 16 билетов на каждой Сколько еще билетов осталось у кассира...