Физика, вопрос задал lpetrova39 , 6 лет назад

Помогите решить задачу!!!

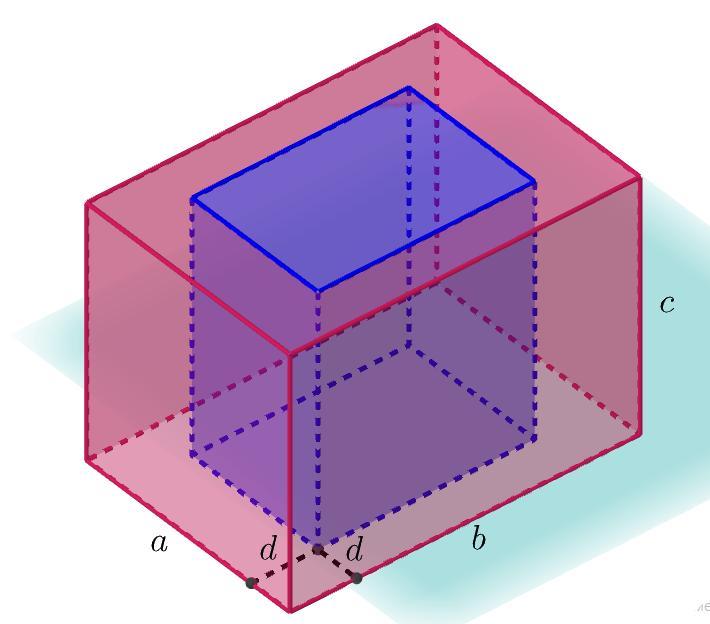
Какова толщина стенки коробки из аллюминия длиной 30 см, шириной 20 см, высотой 10 см и массой 216 гр? Коробка состоит из дна и стенок, крышки она не имеет. Плотность аллюминия 2700 кг/м3

Ответы на вопрос

Ответил mathkot

Ответ:

Толщина стенки $8 \cdot 10^{-4}$ м

Объяснение:

Дано:

a = 0,2 м

b = 0,3 м

с = 0,1 м

m = 0,216 кг

$\rho =$ 2700 кг/м³

Найти:

d - ?

-------------------------------------

Решение:

Считаем, что толщина постоянна.

Объем паралелепипеда есть произведение трех его измерений.

$V -$ объем коробки без учета стенок

$V_{p} -$ объем полости

$зV -$ объем коробки со стенками

$зV = V - V_{p} = abc - (a - 2d)(b - 2d)c = c(ab - ( (a - 2d)(b - 2d))) =$

$= c(ab - ( ab - 2da - 2db + 4d^{2}) =c(ab - ab + 2da + 2db - 4d^{2}) =$

$= c(2da + 2db - 4d^{2}) = 2c(da + db - 2d^{2})$

$\rho = \dfrac{m}{V} \Longrightarrow \boxed{V = \dfrac{m}{\rho} }$

То есть $зV = \dfrac{m}{\rho}$ - объем коробки со стенками

ΔV = 0,216 кг / 2700 кг/м³ = 0,00008 м³

$2c(da + db - 2d^{2}) = зV$

[ΔV] = м³

$2 \cdot 0,1 (0,2d + 0,3d - 2d^{2}) = 0,00008|: (2 \cdot 0,1)$

$0,5d - 2d^{2}= 0,0004$

$2d^{2} - 0,5d + 0,0004 = 0|\cdot 2$

$4d^{2} - d + 0,0008 = 0$

$D = 1 - 4 \cdot 4 \cdot 0,0008 = 0,9872$

$d_{1} = \dfrac{1 - \sqrt{0,9872} }{8} \approx 8 \cdot 10^{-4}$ м

$d_{2} = \dfrac{1 + \sqrt{0,9872} }{8} \approx 0,25$ м - не подходит, так как ширина 0,2 м, а толщина должна быть меньше ширины.

Ответ: Толщина стенки $8 \cdot 10^{-4}$ м.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

правила переноса для слов ужин, улей, урок...

Английский язык, 1 год назад

Sequence of Tenses (согласование времён) Английский 10 класс. Помогите, пожалуйста! Вот текст со скобками. Пожалуйста, раскройте скобки в соответствии с "Sequence of Tenses" Once a famous boxer...

Биология, 6 лет назад

Только для продуцентов в сообществе характерно (несколько вариантов ответа) Задание на фото.

Алгебра, 6 лет назад

знайти область визначення функції y=2x+1...

Математика, 8 лет назад

Найдите 1/19 от суммы чисел 8 1/3 и 1 1/6 . дам 15 баллов.

Геометрия, 8 лет назад

В основании прямого параллелепипеда, лежит ромб со стороной 10см и острым углом 30. Высота параллелепипеда 5см. Найти объём параллелепипеда.